The DeCAMFounder: Non-Linear Causal Discovery in the Presence of Hidden Variables

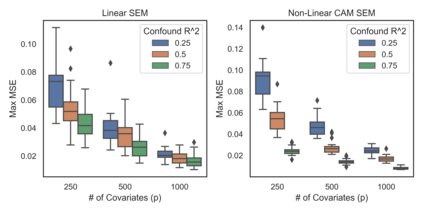
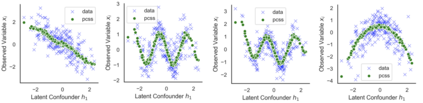
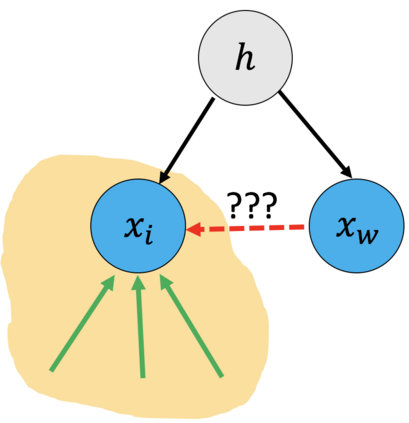
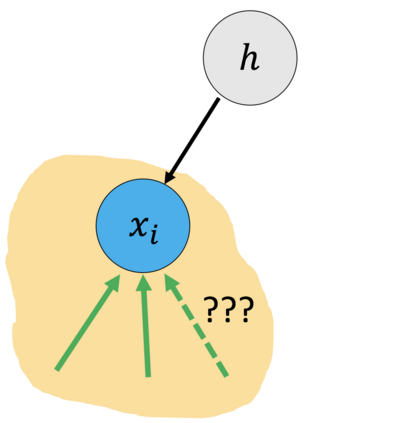
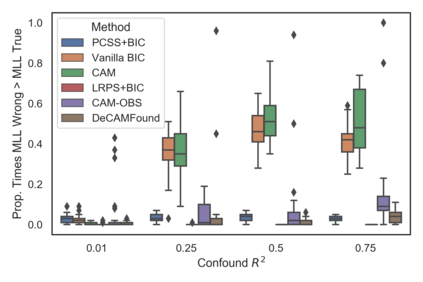
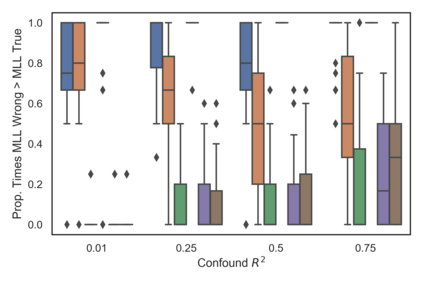
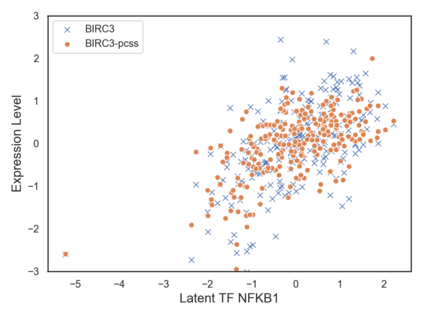
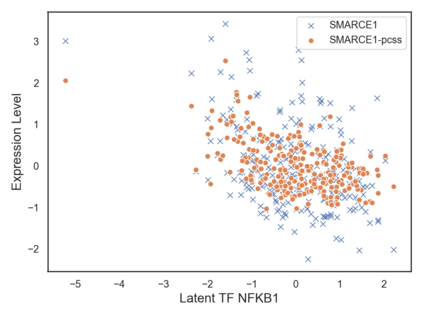
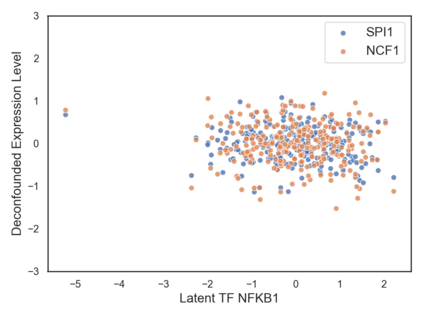
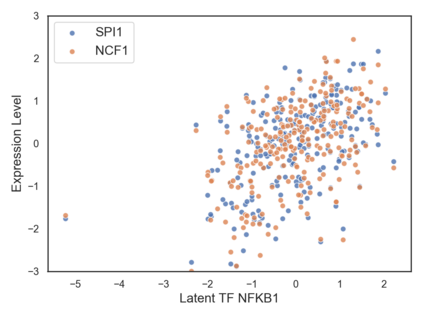
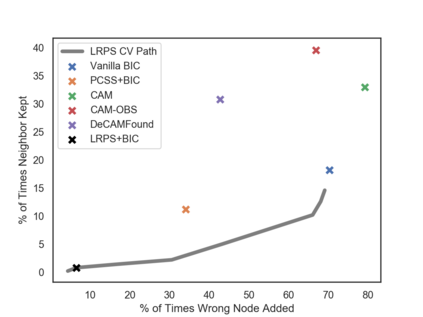
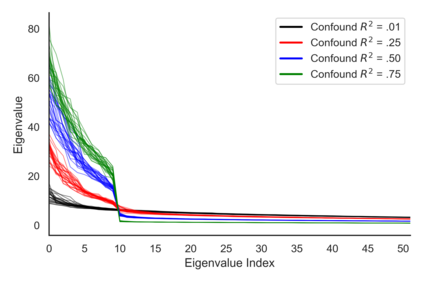
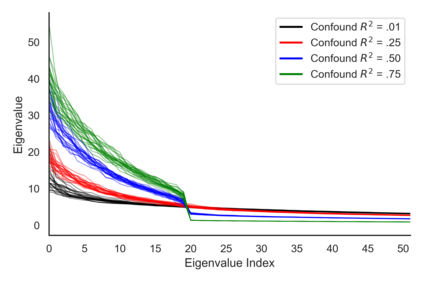
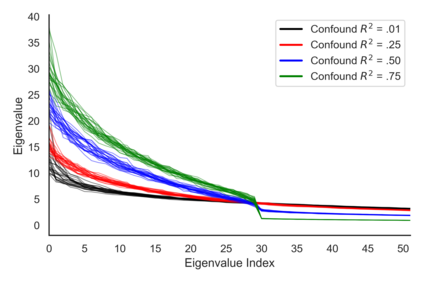
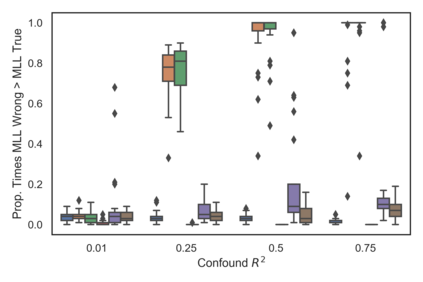
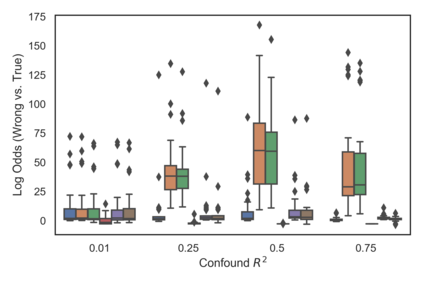
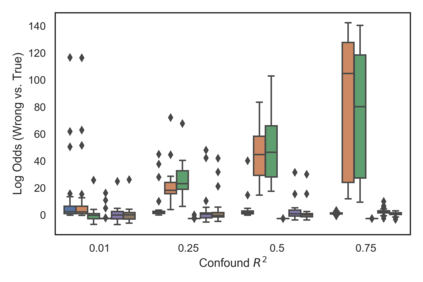
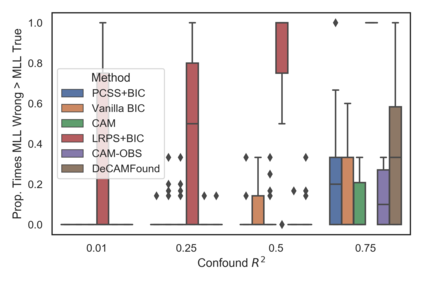
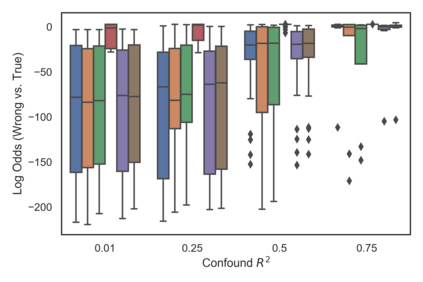
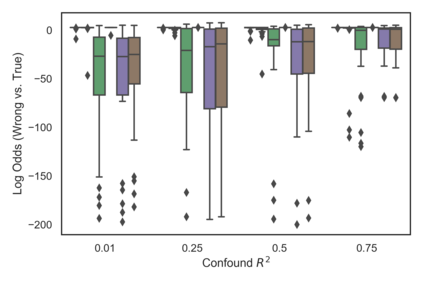
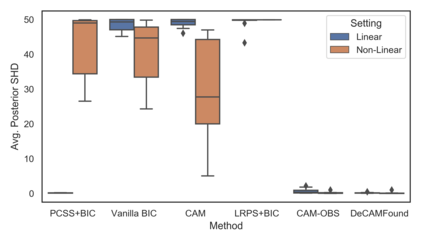
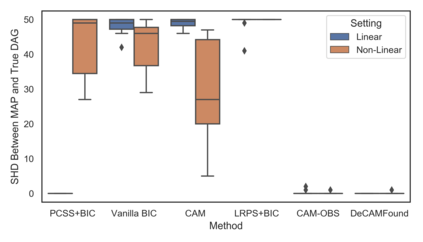
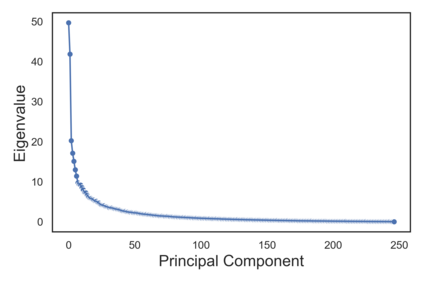
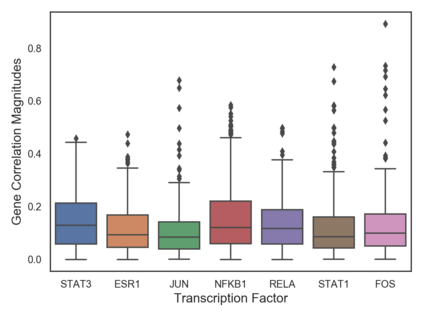
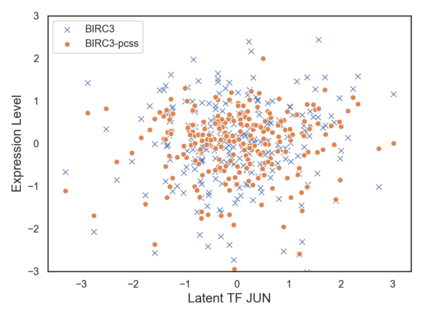
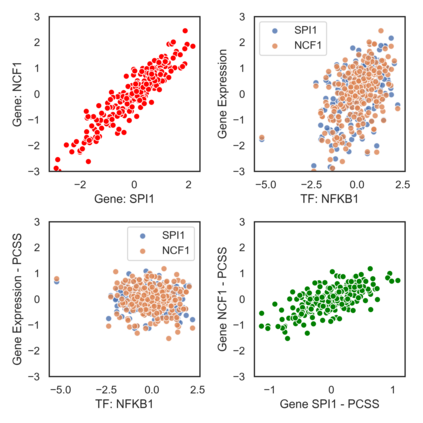
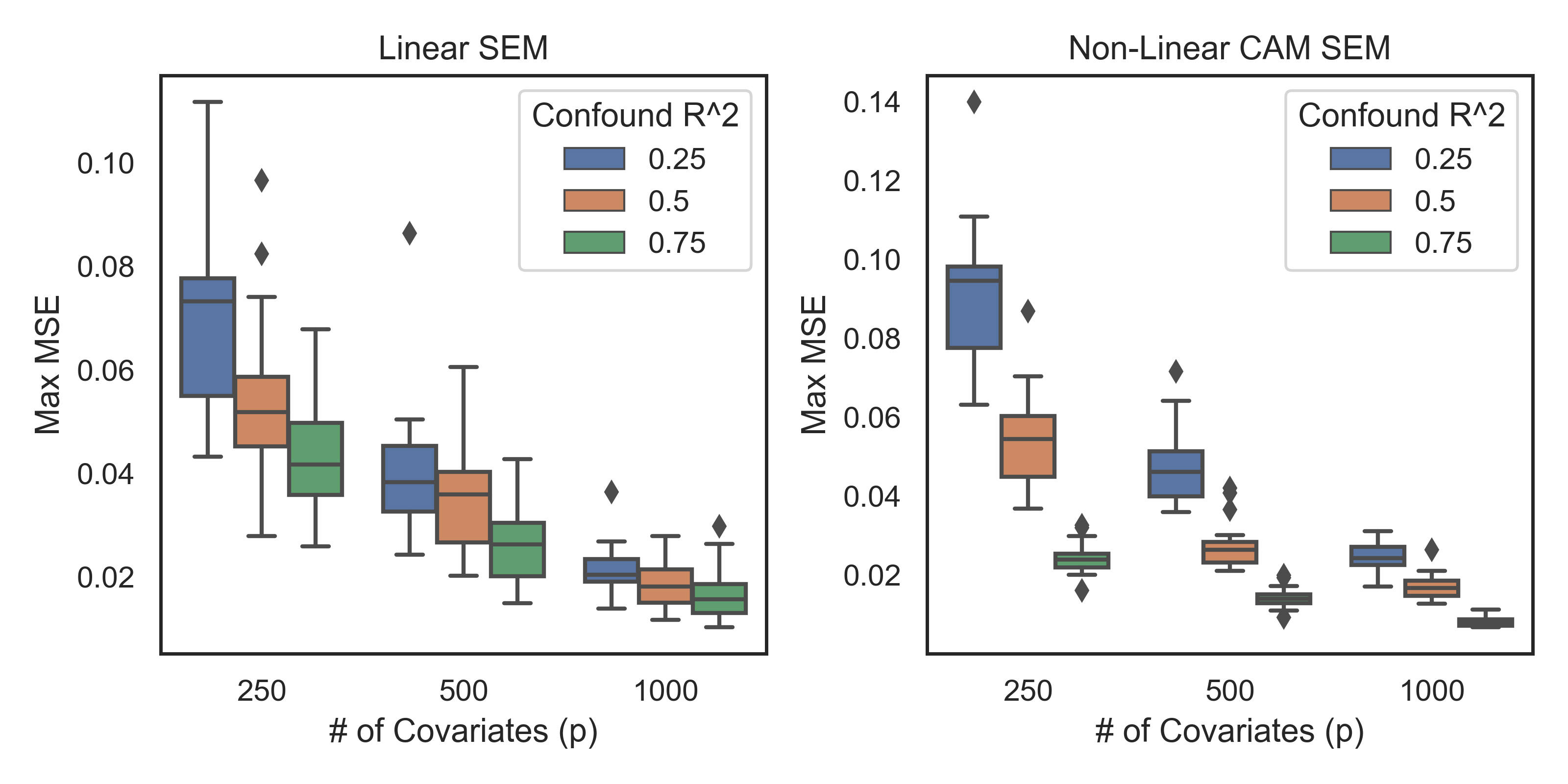
Many real-world decision-making tasks require learning causal relationships between a set of variables. Typical causal discovery methods, however, require that all variables are observed, which might not be realistic in practice. Unfortunately, in the presence of latent confounding, recovering causal relationships from observational data without making additional assumptions is an ill-posed problem. Fortunately, in practice, additional structure among the confounders can be expected, one such example being pervasive confounding, which has been exploited for consistent causal estimation in the special case of linear causal models. In this paper, we provide a proof and consistent method to estimate causal relationships in the non-linear, pervasive confounding setting. The heart of our procedure relies on the ability to estimate the confounding variation through a simple spectral decomposition of the observed data matrix. We derive a DAG score function based on this insight, prove its consistency in recovering a correct ordering of the DAG, and empirically compare it to existing procedures. We show improved performance on both simulated and real datasets by explicitly accounting for both confounders and non-linear effects.