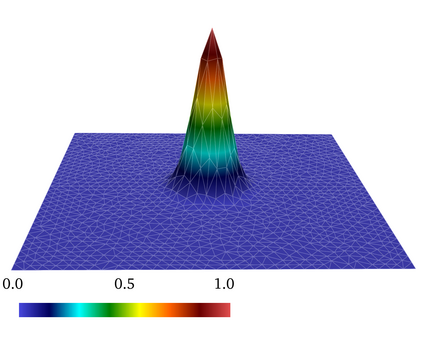
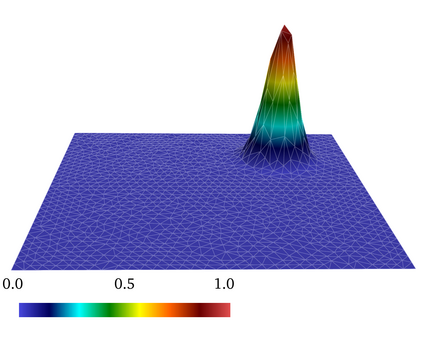
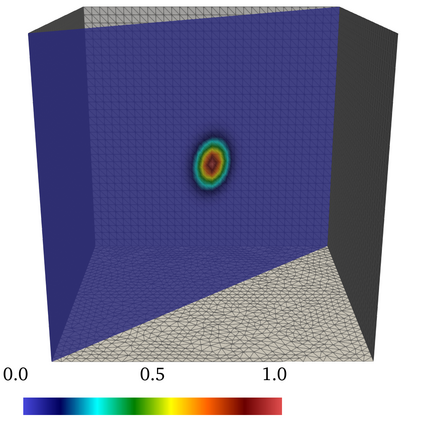
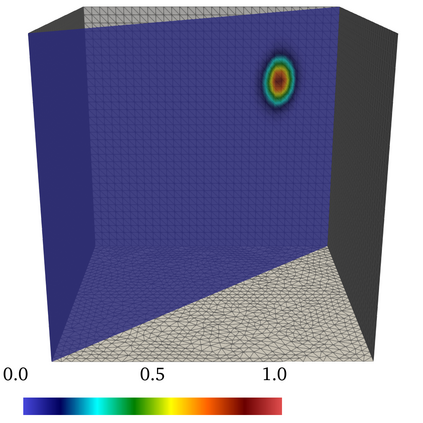
A mass-conservative Lagrange--Galerkin scheme of second order in time for convection-diffusion problems

A mass-conservative Lagrange--Galerkin scheme of second order in time for convection-diffusion problems is presented, and convergence with optimal error estimates is proved in the framework of $L^2$-theory. The introduced scheme maintains the advantages of the Lagrange--Galerkin method, i.e., CFL-free robustness for convection-dominated problems and a symmetric and positive coefficient matrix resulting from the discretization. In addition, the scheme conserves the mass on the discrete level. Unconditional stability and error estimates of second order in time are proved by employing two new key lemmas on the truncation error of the material derivative in conservative form and on a discrete Gronwall inequality for multistep methods. The mass-conservation property is achieved by the Jacobian multiplication technique introduced by Rui and Tabata in 2010, and the accuracy of second order in time is obtained based on the idea of the multistep Galerkin method along characteristics originally introduced by Ewing and Russel in 1981. For the first time step, the mass-conservative scheme of first order in time by Rui and Tabata in 2010 is employed, which is efficient and does not cause any loss of convergence order in the $\ell^\infty(L^2)$- and $\ell^2(H^1_0)$-norms. For the time increment $\Delta t$, the mesh size $h$ and a conforming finite element space of polynomial degree $k$, the convergence order is of $O(\Delta t^2 + h^k)$ in the $\ell^\infty(L^2)\cap \ell^2(H^1_0)$-norm and of $O(\Delta t^2 + h^{k+1})$ in the $\ell^\infty(L^2)$-norm if the duality argument can be employed. Error estimates of $O(\Delta t^{3/2}+h^k)$ in discrete versions of the $L^\infty(H^1_0)$- and $H^1(L^2)$-norm are additionally proved. Numerical results confirm the theoretical convergence orders in one, two and three dimensions.