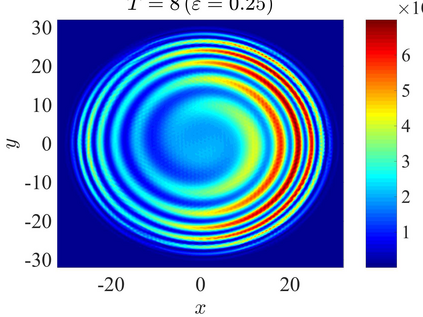
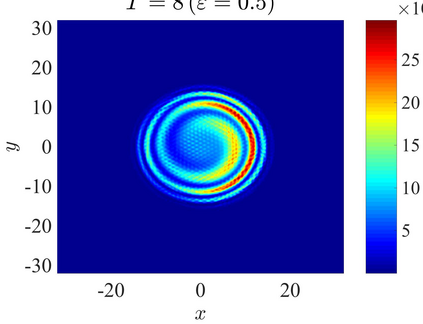
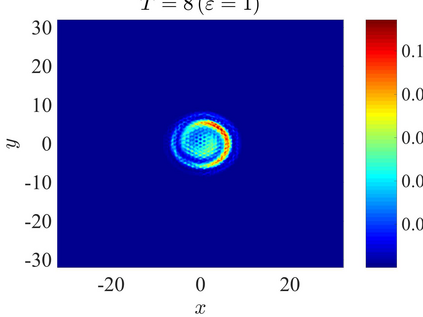
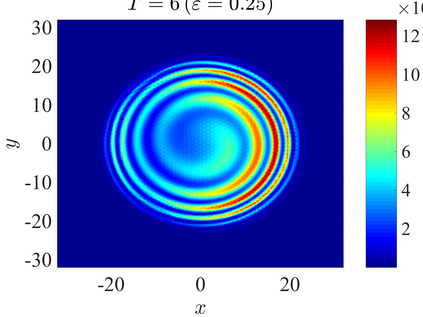
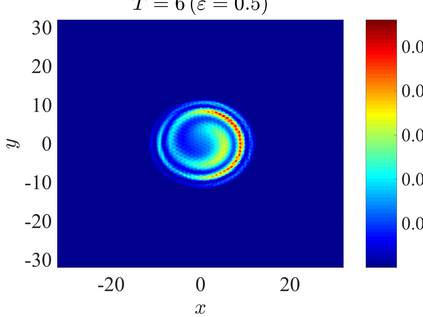
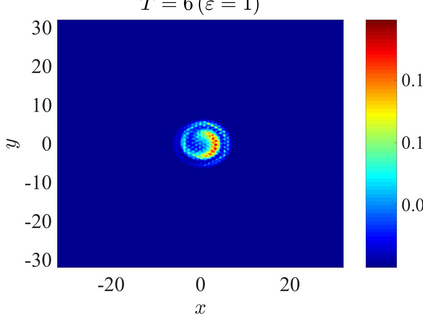
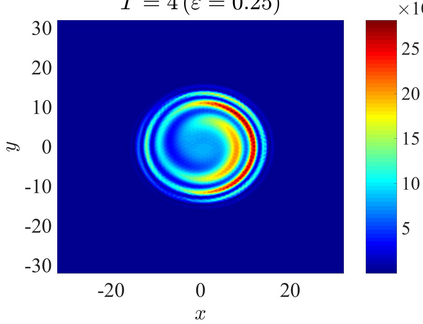
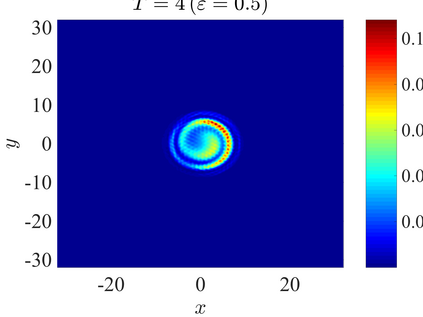
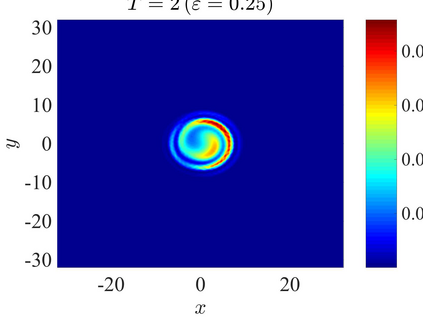
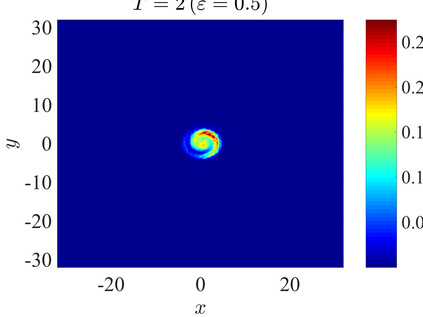
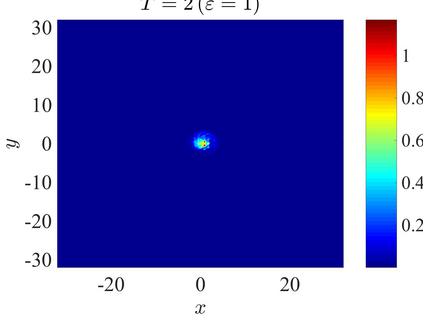
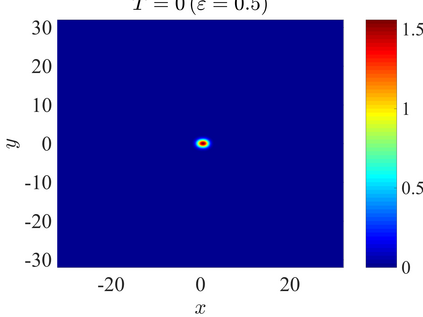
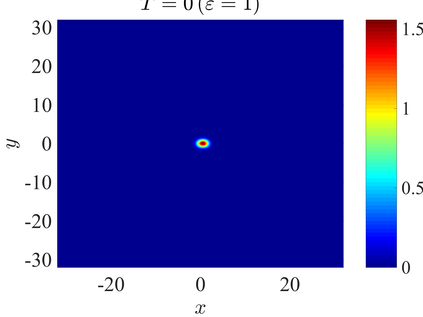
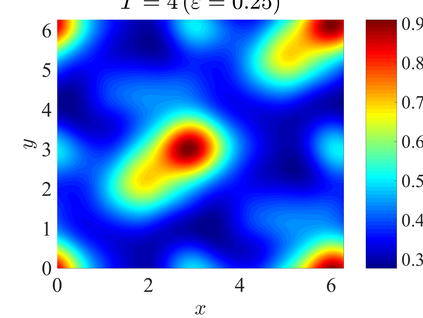
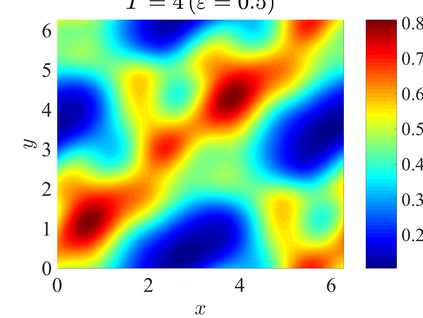
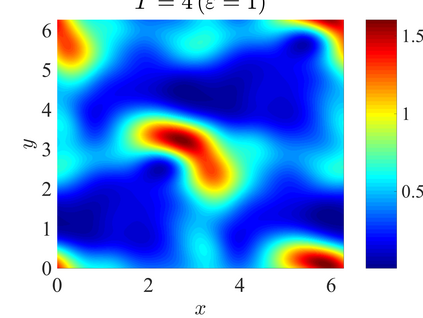
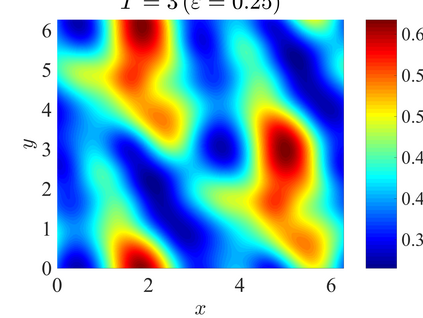
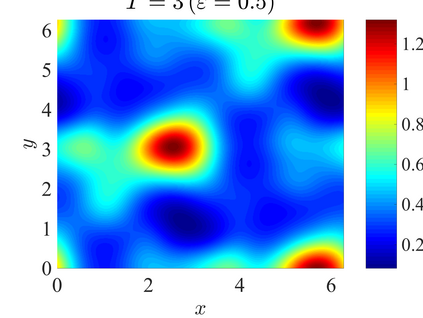
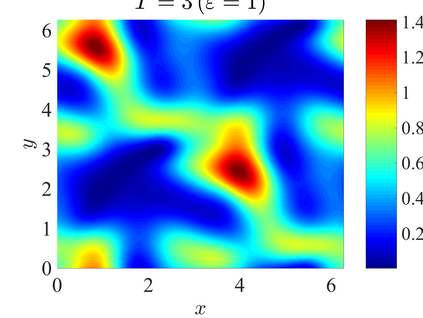
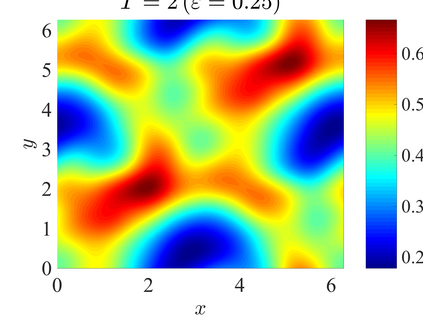
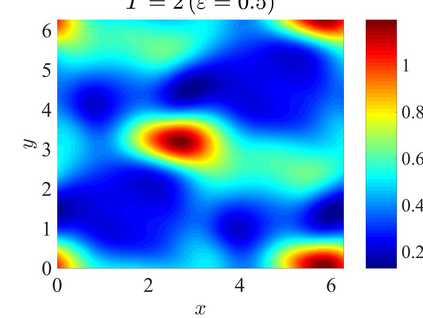
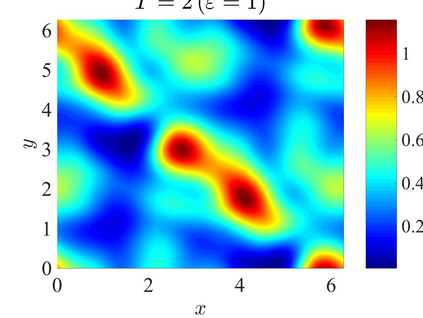
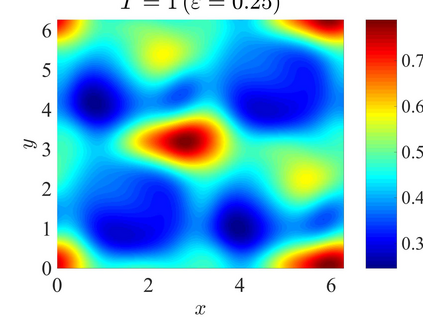
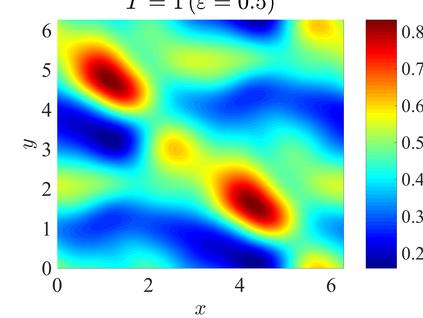
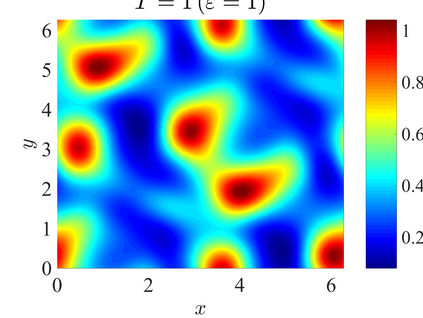
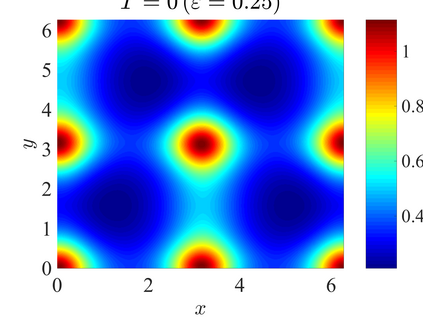
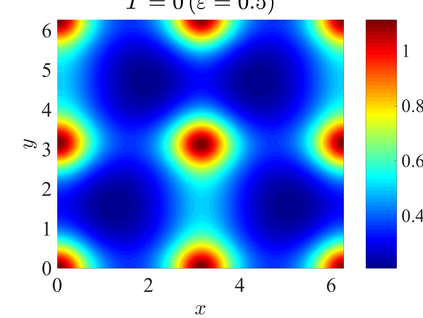
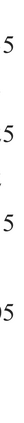We establish the error bounds of fourth-order compact finite difference (4cFD) methods for the Dirac equation in the massless and nonrelativistic regime, which involves a small dimensionless parameter $0 < \varepsilon \le 1$ inversely proportional to the speed of light. In this regime, the solution propagates waves with wavelength $O(\varepsilon)$ in time and $O(1)$ in space, as well as with the wave speed $O(1/\varepsilon)$ rapid outgoing waves. We adapt the conservative and semi-implicit 4cFD methods to discretize the Dirac equation and rigorously carry out their error bounds depending explicitly on the mesh size $h$, time step $\tau$ and the small parameter $\varepsilon$. Based on the error bounds, the $\varepsilon$-scalability of the 4cFD methods is $h = O(\varepsilon^{1/4})$ and $\tau = O(\varepsilon^{3/2})$, which not only improves the spatial resolution capacity but also has superior accuracy than classical second-order finite difference methods. Furthermore, physical observables including the total density and current density have the same conclusions. Numerical results are provided to validate the error bounds and the dynamics of the Dirac equation with different potentials in 2D is presented.
翻译:我们为无质量和非相对性制度中的Dirac 方程式确定了四级压缩定值差异(4cFD)方法的误差界限(4cFD),这涉及一个小的无维参数 $0 < \ varepsilon\le 1美元,与光速成反比。在这个制度中,解决方案以波长O(\ varepsilon) 美元和空间美元传播波浪,以及波速O(1/\ varepsilon) 美元快速流出波速。我们调整保守的和半隐含的4cFD 方法,以便将Dirac 方程式分离,并严格执行其误差界限,明确取决于网形大小$(h) 美元、 时间级($tau) 美元和小参数($\ varepsilon) 美元。根据错误界限,4cFD方法的可缩放值是$h (Oh) = O(\\ varepsilalislon) 1/4} 和 美元= O(vrealalalalalalalalalal-rassim reck) exalization ex exlate ex ex ex ex ex exmlations),但不提供不改进了当前硬度(c) 10xxxilentalislismlismildismexxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx