A polynomial time construction of a hitting set for read-once branching programs of width 3

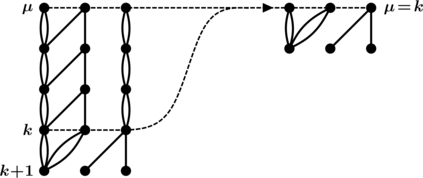
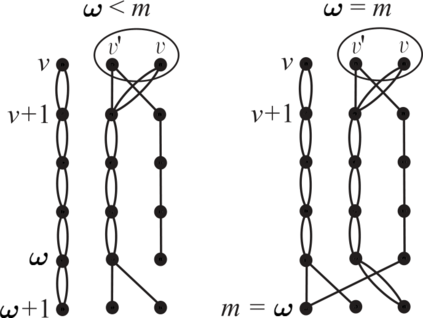
Recently, an interest in constructing pseudorandom or hitting set generators for restricted branching programs has increased, which is motivated by the fundamental issue of derandomizing space-bounded computations. Such constructions have been known only in the case of width 2 and in very restricted cases of bounded width. In this paper, we characterize the hitting sets for read-once branching programs of width 3 by a so-called richness condition. Namely, we show that such sets hit the class of read-once conjunctions of DNF and CNF (i.e. the weak richness). Moreover, we prove that any rich set extended with all strings within Hamming distance of 3 is a hitting set for read-once branching programs of width 3. Then, we show that any almost $O(\log n)$-wise independent set satisfies the richness condition. By using such a set due to Alon et al. (1992) our result provides an explicit polynomial time construction of a hitting set for read-once branching programs of width 3 with acceptance probability $\varepsilon>5/6$. We announced this result at conferences almost 10 years ago, including only proof sketches, which motivated a plenty of subsequent results on pseudorandom generators for restricted read-once branching programs. This paper contains our original detailed proof that has not been published yet.