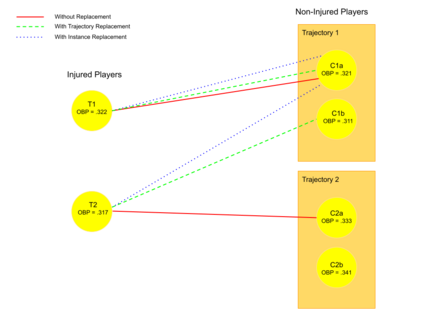
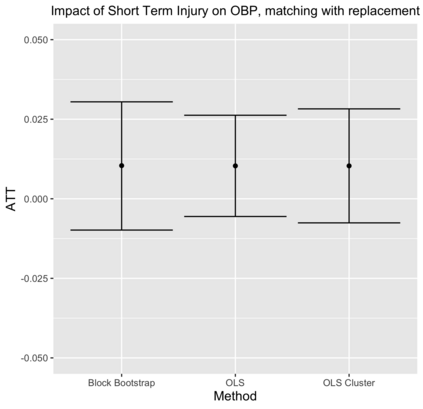
Matching in observational studies faces complications when units enroll in treatment on a rolling basis. While each treated unit has a specific time of entry into the study, control units each have many possible comparison, or "pseudo-treatment," times. The recent GroupMatch framework (Pimentel et al., 2020) solves this problem by searching over all possible pseudo-treatment times for each control and selecting those permitting the closest matches based on covariate histories. However, valid methods of inference have been described only for special cases of the general GroupMatch design, and these rely on strong assumptions. We provide three important innovations to address these problems. First, we introduce a new design, GroupMatch with instance replacement, that allows additional flexibility in control selection and proves more amenable to analysis. Second, we propose a block bootstrap approach for inference in GroupMatch with instance replacement and demonstrate that it accounts properly for complex correlations across matched sets. Third, we develop a permutation-based falsification test to detect possible violations of the important timepoint agnosticism assumption underpinning GroupMatch, which requires homogeneity of potential outcome means across time. Via simulation and a case study of the impact of short-term injuries on batting performance in major league baseball, we demonstrate the effectiveness of our methods for data analysis in practice.
翻译:在观测研究中,匹配的单位面临在滚动基础上进行治疗的复杂情况。虽然每个处理过的单位都有进入研究的具体时间,但每个控制单位都有许多可能的比较或“假待遇”的时间。最近的GroupMatch框架(Pimentel等人,2020年)通过搜索每一种控制的所有可能的伪治疗时间和根据共变历史选择最接近匹配的单位来解决了这一问题。然而,只对一般组配设计的特殊案例说明了有效的推断方法,这些假设依赖于强有力的假设。我们提供了三种重要的创新,以解决这些问题。首先,我们采用了一种新的设计,即“组配对实例替换”,允许在控制选择方面有更大的灵活性,并证明更便于分析。第二,我们建议了一种块式套套方法,用以在组配对的每次控制中查找所有可能的伪治疗时间,并证明它能正确反映相匹配的各组之间的复杂关系。第三,我们开发了基于变相测试的根据短期假假设,以发现可能违反重要时间点的假设情况。我们为G组配配的假设提供了三种重要的创新。首先,我们引入了一种新的设计,即组合配对实例的组合组合配配,要求在控制选择选择中具有同性,在选择选择中具有更大的灵活性,在选择中允许性,在选择中具有更大的结果影响,从而可以展示性,从而显示我们的主要结果结果的模拟,从而显示我们的主要结果分析方法,从而显示我们对等的模拟的实验性分析方法,从而显示我们对等的实验结果的影响。我们对等的功能的模拟的实验性分析方法,从而展示了对等的实验性分析方法,我们对等性能对等的实验性能对等。我们对等性研究。我们对等性研究。我们对等性研究。我们对等性分析了对等性分析了对等性研究。我们对等性的研究。我们对等性研究。