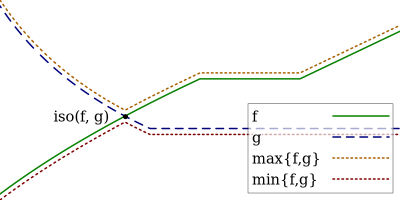
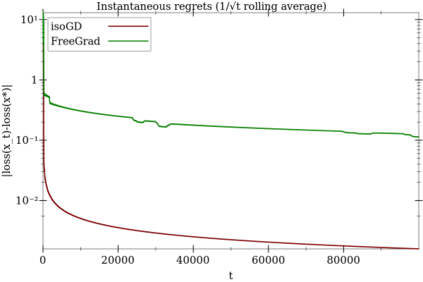
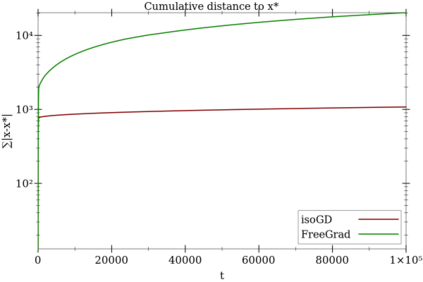
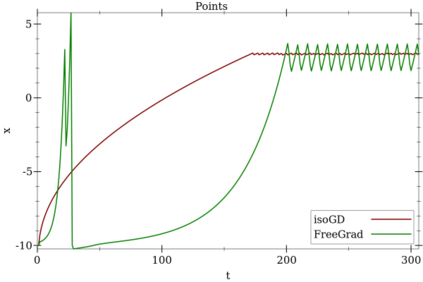
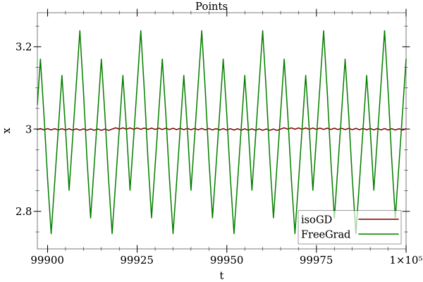
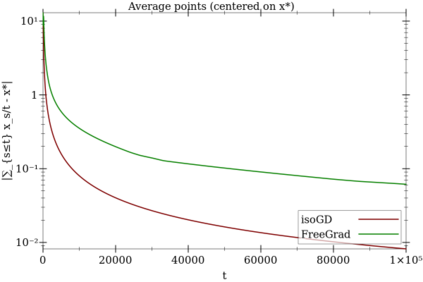
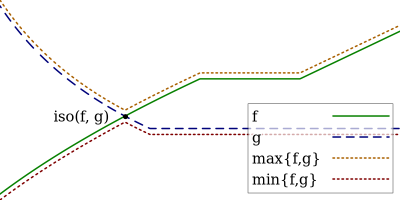
We extend and combine several tools of the literature to design fast, adaptive, anytime and scale-free online learning algorithms. Scale-free regret bounds must scale linearly with the maximum loss, both toward large losses and toward very small losses. Adaptive regret bounds demonstrate that an algorithm can take advantage of easy data and potentially have constant regret. We seek to develop fast algorithms that depend on as few parameters as possible, in particular they should be anytime and thus not depend on the time horizon. Our first and main tool, isotuning, is a generalization of the idea of balancing the trade-off of the regret. We develop a set of tools to design and analyze such learning rates easily and show that they adapts automatically to the rate of the regret (whether constant, $O(\log T)$, $O(\sqrt{T})$, etc.) within a factor 2 of the optimal learning rate in hindsight for the same observed quantities. The second tool is an online correction, which allows us to obtain centered bounds for many algorithms, to prevent the regret bounds from being vacuous when the domain is overly large or only partially constrained. The last tool, null updates, prevents the algorithm from performing overly large updates, which could result in unbounded regret, or even invalid updates. We develop a general theory using these tools and apply it to several standard algorithms. In particular, we (almost entirely) restore the adaptivity to small losses of FTRL for unbounded domains, design and prove scale-free adaptive guarantees for a variant of Mirror Descent (at least when the Bregman divergence is convex in its second argument), extend Adapt-ML-Prod to scale-free guarantees, and provide several other minor contributions about Prod, AdaHedge, BOA and Soft-Bayes.
翻译:我们扩展和合并了若干文献工具,以设计快速、适应性、随时和无比例的在线学习算法。 无规模的遗憾界限必须随着最大损失而直线缩放,包括巨大的损失和极小的损失。 适应性遗憾界限表明, 算法可以利用简单数据, 并有可能不断感到后悔。 我们试图开发一些取决于尽可能少的参数的快速算法, 特别是它们应该有时间, 从而不取决于时间范围。 我们的第一和主要工具正在调整, 是平衡遗憾交易的理念的概括化。 我们开发了一套工具, 来设计和分析这种最大损失, 容易导致巨大的损失。 当局域内没有多少争论, 美元( ) 美元( ) 美元( 美元) 美元( 美元) 美元( 美元) ( 美元) ( 美元) ( 美元) ( 美元) ( 美元) ( 美元) ( 美元) ( 美元) ( 美元) ( 美元) ( 美元) ( 美元) ( ) ( ) ( ) ( ) ( 我们试图( 相同数量( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 相同) ( ) ( ) ( 相同) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )