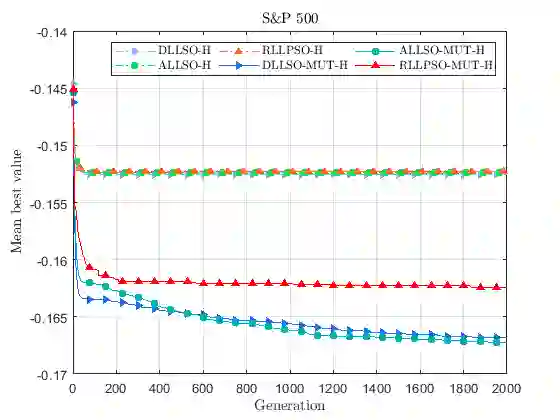
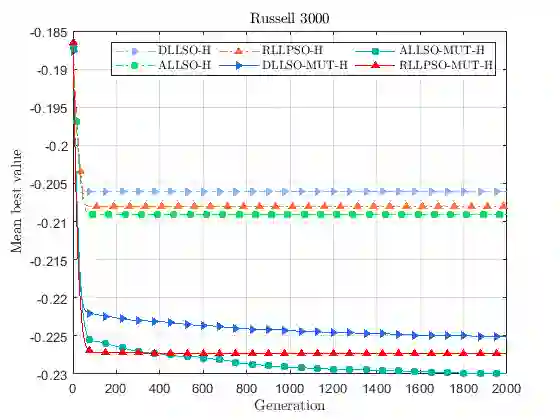
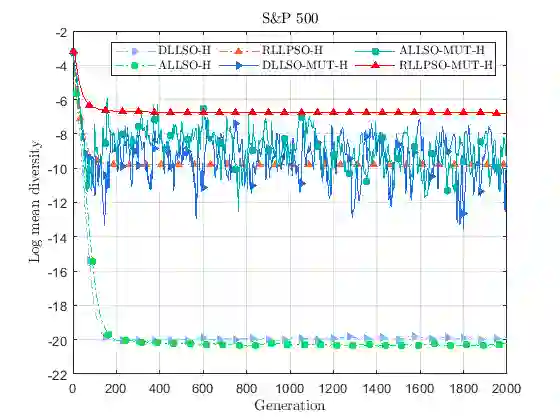
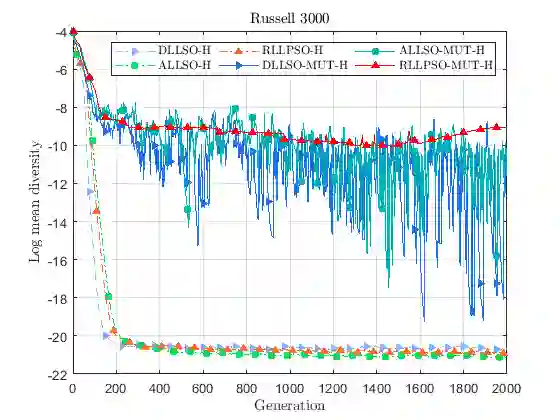
In this work, we propose a hybrid variant of the level-based learning swarm optimizer (LLSO) for solving large-scale portfolio optimization problems. Our goal is to maximize a modified formulation of the Sharpe ratio subject to cardinality, box and budget constraints. The algorithm involves a projection operator to deal with these three constraints simultaneously and we implicitly control transaction costs thanks to a rebalancing constraint. We also introduce a suitable exact penalty function to manage the turnover constraint. In addition, we develop an ad hoc mutation operator to modify candidate exemplars in the highest level of the swarm. The experimental results, using three large-scale data sets, show that the inclusion of this procedure improves the accuracy of the solutions. Then, a comparison with other variants of the LLSO algorithm and two state-of-the-art swarm optimizers points out the outstanding performance of the proposed solver in terms of exploration capabilities and solution quality. Finally, we assess the profitability of the portfolio allocation strategy in the last five years using an investible pool of 1119 constituents from the MSCI World Index.
翻译:在这项工作中,我们提出一个基于水平的学习群优化器(LLSO)的混合变体,以解决大规模组合优化问题。我们的目标是在受基本因素、箱和预算限制的情况下,最大限度地扩大对Sharpe比率的修改配方。算法涉及一个同时处理这三个制约因素的预测操作员,我们因再平衡的制约而隐含地控制交易费用。我们还引入一个适当的精确罚款功能来管理更替限制。此外,我们开发了一个特设突变操作员,以修改群中最高层的候选成像器。实验结果利用三个大型数据集,表明这一程序的纳入提高了解决方案的准确性。然后,与LSO算法的其他变体和两个最先进的温优化器进行比较,指出拟议的解决方案在勘探能力和解决方案质量方面的杰出表现。最后,我们利用来自MSCI世界指数的1119个可投资选民群评估了过去五年中组合分配战略的利润。