Lévy Adaptive B-spline Regression via Overcomplete Systems

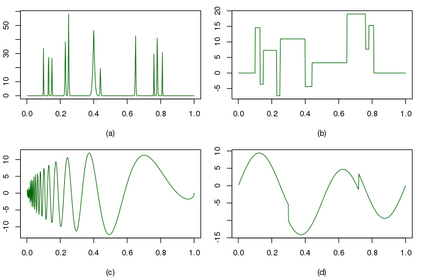
The estimation of functions with varying degrees of smoothness is a challenging problem in the nonparametric function estimation. In this paper, we propose the LABS (L\'{e}vy Adaptive B-Spline regression) model, an extension of LARK and LARMuK models, for the estimation of functions with varying degrees of smoothness. LABS model is a LARK with B-spline bases as generating kernels. The B-spline basis consists of piecewise k degree polynomials with k-1 continuous derivatives and can express systematically functions with varying degrees of smoothness. By changing the orders of the B-spline basis, LABS can systematically adapt the smoothness of functions, i.e., jump discontinuities, sharp peaks, etc. Results of simulation studies and real data examples support that this model catches not only smooth areas but also jumps and sharp peaks of functions. The proposed model also has the best performance in almost all examples. Finally, we provide theoretical results that the mean function for the LABS model belongs to the certain Besov spaces based on the orders of the B-spline basis and that the prior of the model has the full support on the Besov spaces.