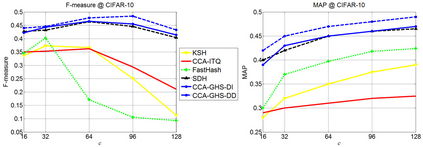
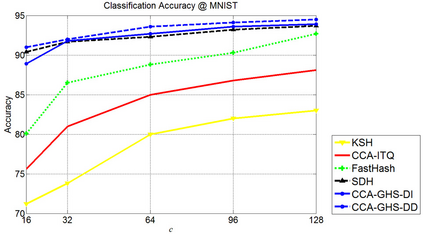
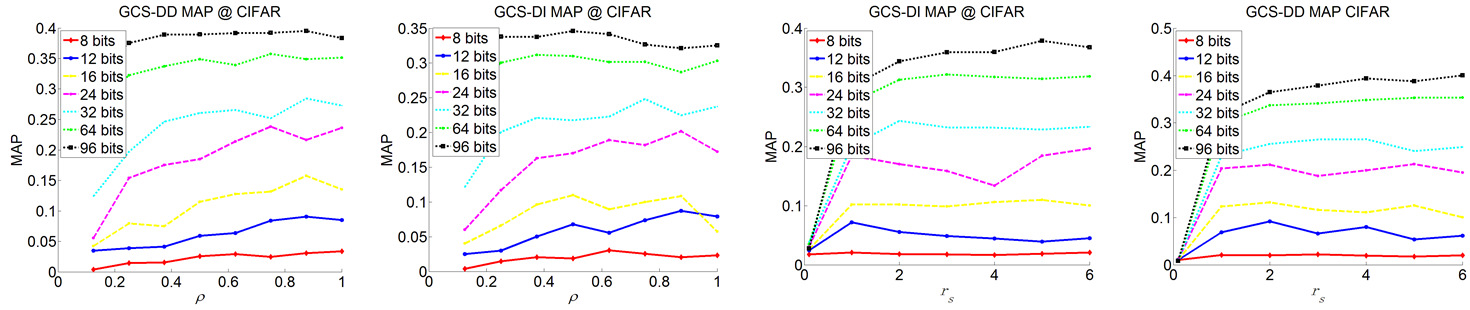
Hashing methods have been widely investigated for fast approximate nearest neighbor searching in large data sets. Most existing methods use binary vectors in lower dimensional spaces to represent data points that are usually real vectors of higher dimensionality. We divide the hashing process into two steps. Data points are first embedded in a low-dimensional space, and the global positioning system method is subsequently introduced but modified for binary embedding. We devise dataindependent and data-dependent methods to distribute the satellites at appropriate locations. Our methods are based on finding the tradeoff between the information losses in these two steps. Experiments show that our data-dependent method outperforms other methods in different-sized data sets from 100k to 10M. By incorporating the orthogonality of the code matrix, both our data-independent and data-dependent methods are particularly impressive in experiments on longer bits.
翻译:对于在大型数据集中快速近距离近邻搜索的散列方法已经进行了广泛调查。大多数现有方法都使用低维空间的二进制矢量来代表通常为较高维度的真正矢量的数据点。我们将散列过程分为两个步骤。数据点首先嵌入低维空间,随后引入了全球定位系统方法,但又作了二进制嵌入修改。我们设计了数据独立和数据独立的方法来在适当地点分配卫星。我们的方法基于在这两个步骤中找出信息损失之间的权衡。实验表明,我们的数据依赖方法在100k至10M不同尺寸数据集中优于其他方法。通过将代码矩阵的正反方向纳入代码矩阵,我们的数据依赖和数据依赖方法在较长的位数实验中特别令人印象深刻。