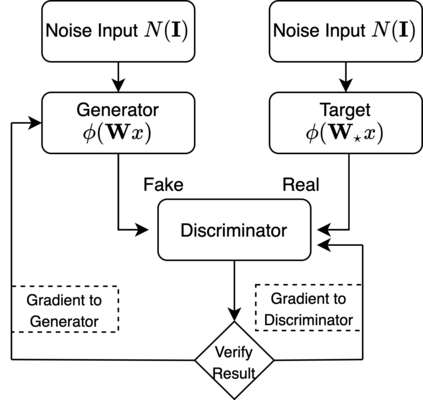
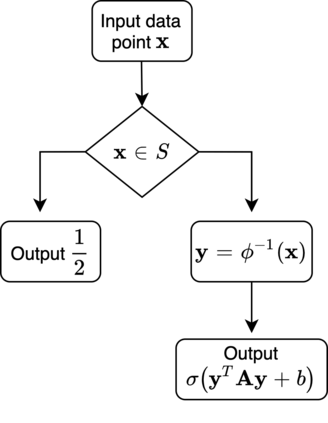
We provide theoretical convergence guarantees on training Generative Adversarial Networks (GANs) via SGD. We consider learning a target distribution modeled by a 1-layer Generator network with a non-linear activation function $\phi(\cdot)$ parametrized by a $d \times d$ weight matrix $\mathbf W_*$, i.e., $f_*(\mathbf x) = \phi(\mathbf W_* \mathbf x)$. Our main result is that by training the Generator together with a Discriminator according to the Stochastic Gradient Descent-Ascent iteration proposed by Goodfellow et al. yields a Generator distribution that approaches the target distribution of $f_*$. Specifically, we can learn the target distribution within total-variation distance $\epsilon$ using $\tilde O(d^2/\epsilon^2)$ samples which is (near-)information theoretically optimal. Our results apply to a broad class of non-linear activation functions $\phi$, including ReLUs and is enabled by a connection with truncated statistics and an appropriate design of the Discriminator network. Our approach relies on a bilevel optimization framework to show that vanilla SGDA works.
翻译:我们通过SGD为培训产生反转网络(GANs)提供理论趋同保证。 我们考虑学习一个目标分布模式,由1级发电机网络和分流器一起培训,其模型是非线性启动功能$\ph(cdot)$(cdot) 的匹配,其模型是美元d = 美元= 美元= 美元= 美元= 美元= 美元= (mathbf W ⁇ \\\ mathbfxx) =\ fi(mathbf W ⁇ \ mathbxx) 。我们的主要结果是,根据Goodfellow 等人提议的Stochatical Emple-Acent Excenteration, 其模型分布将接近于美元=美元= 美元= 美元= 美元= = $\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\