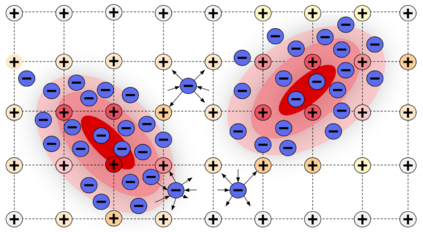
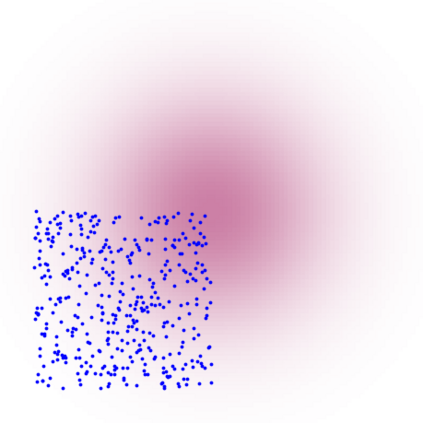
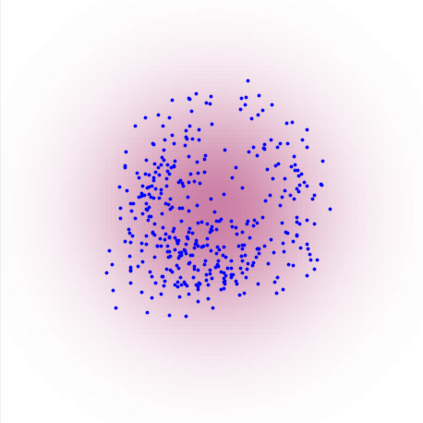
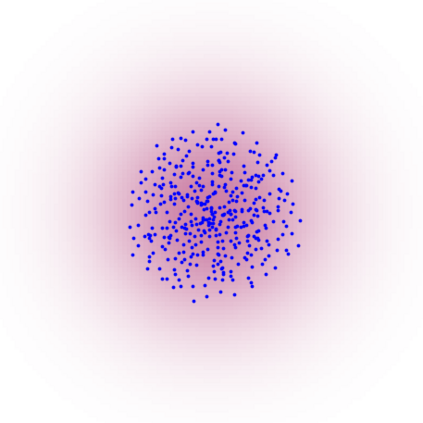
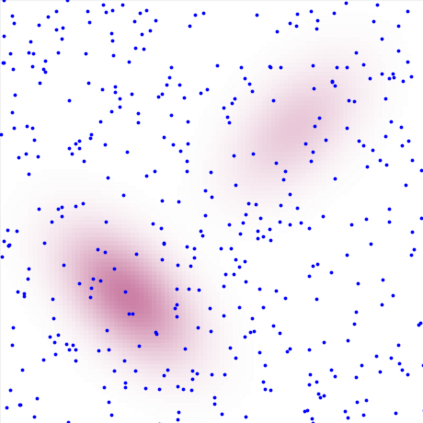
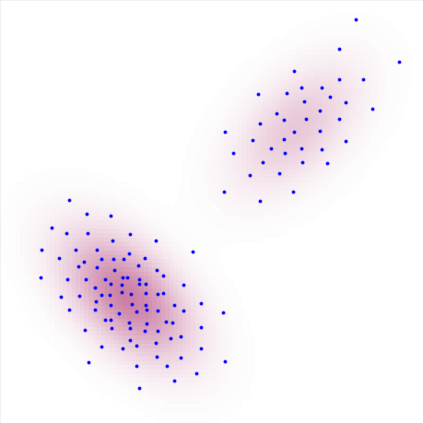
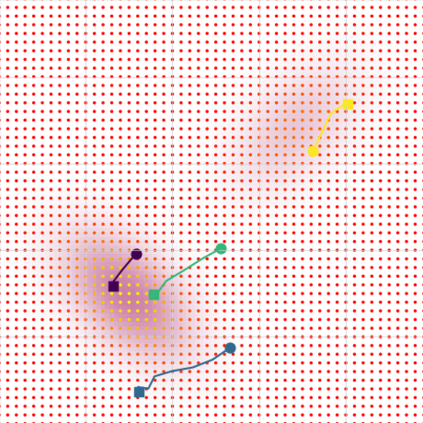
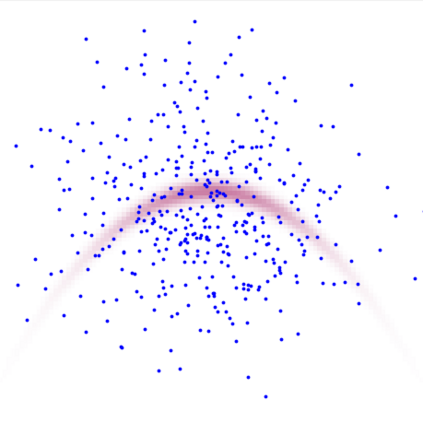
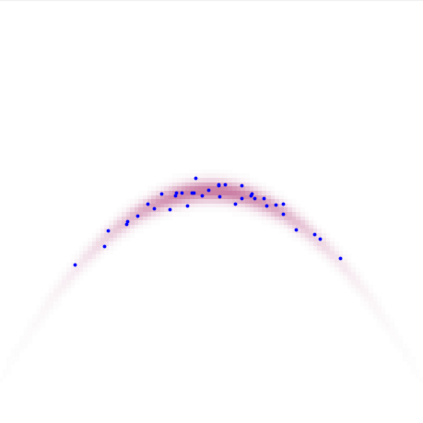
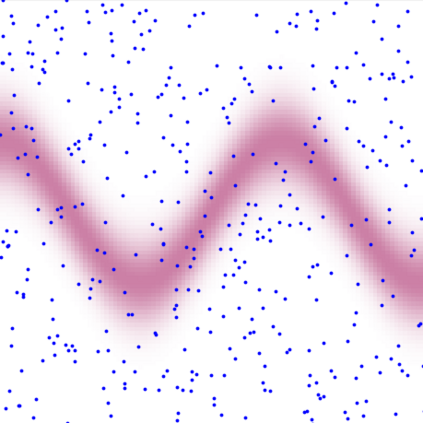
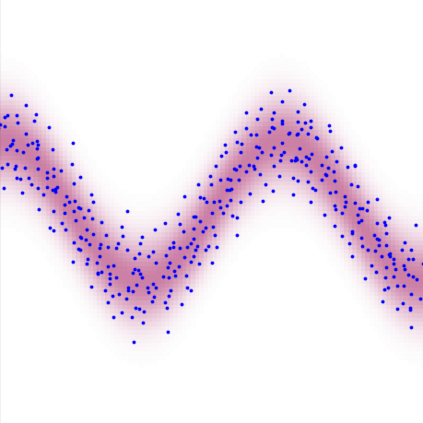
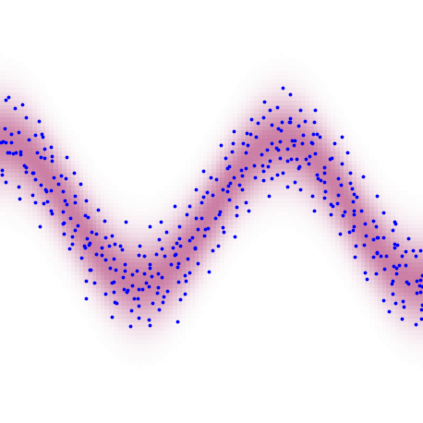
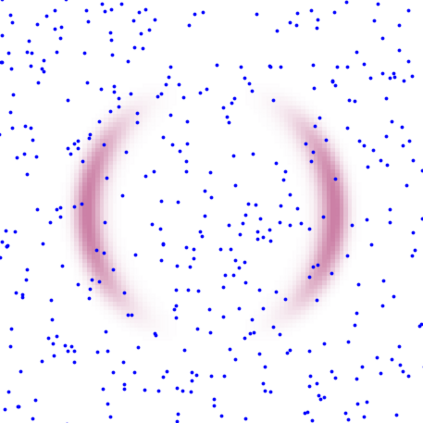
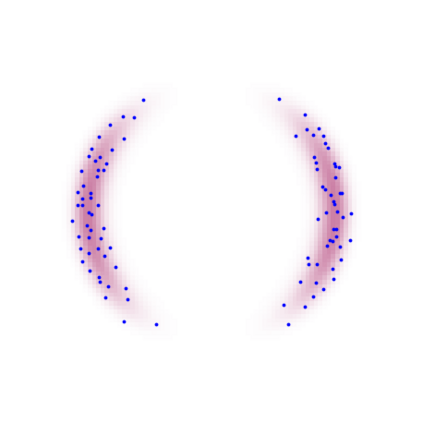
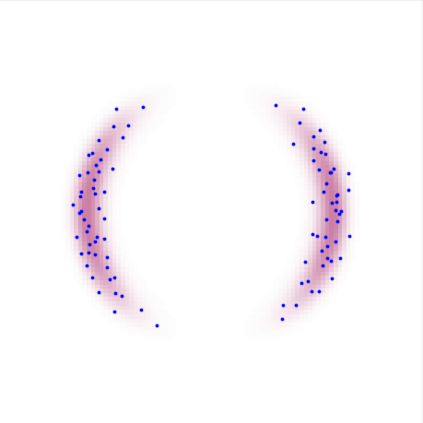
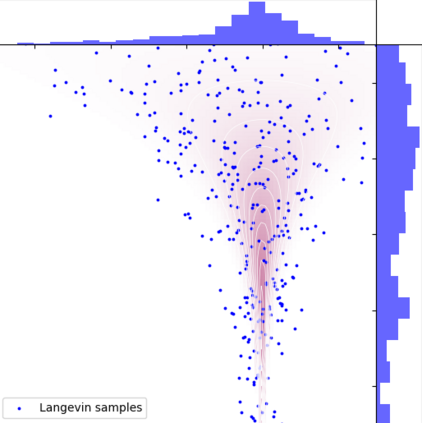
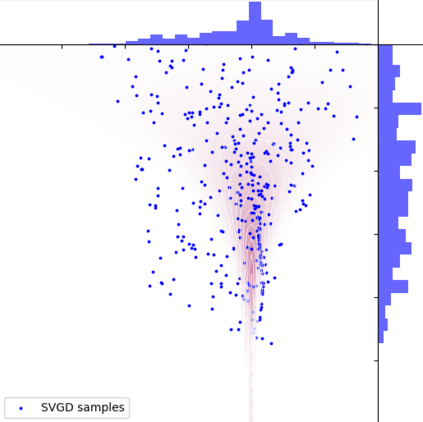
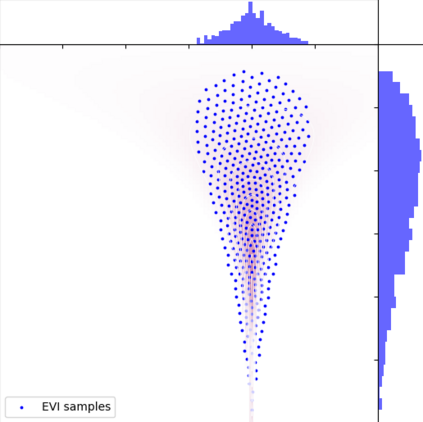
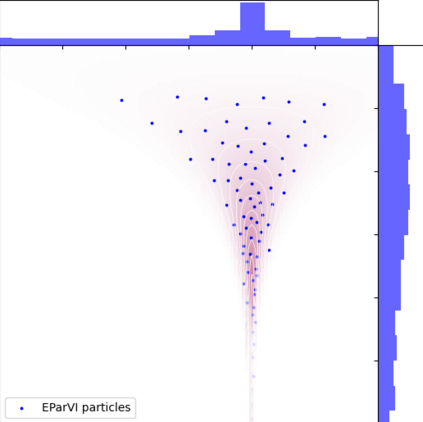
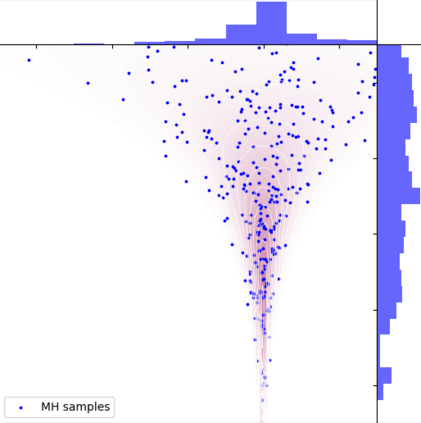
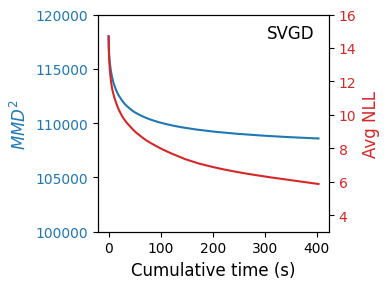
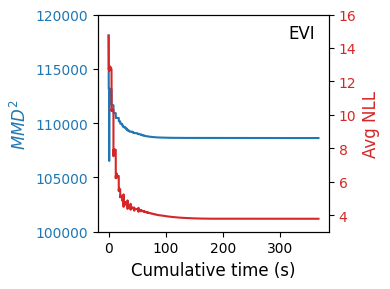
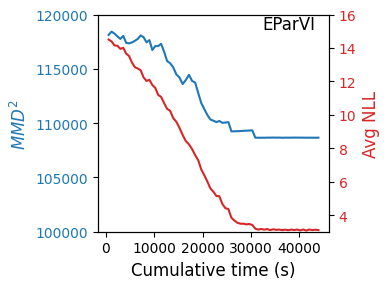
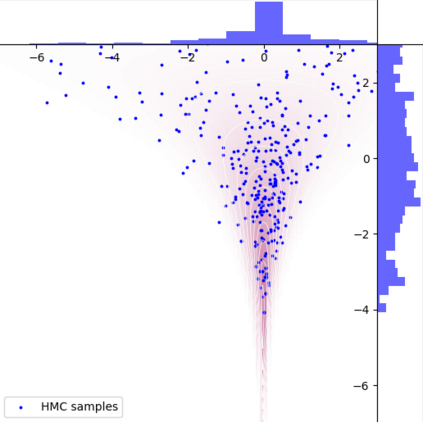
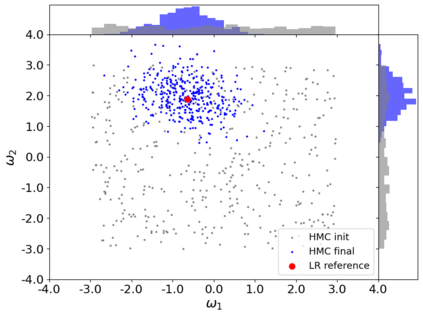
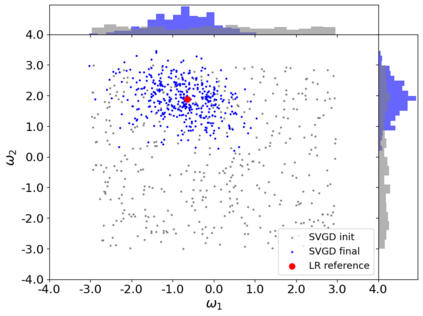
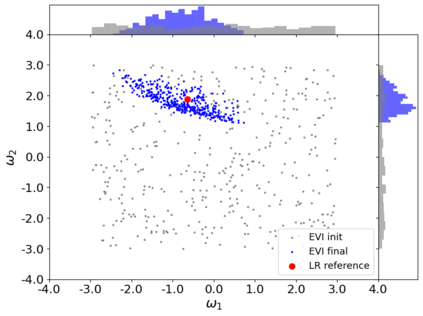
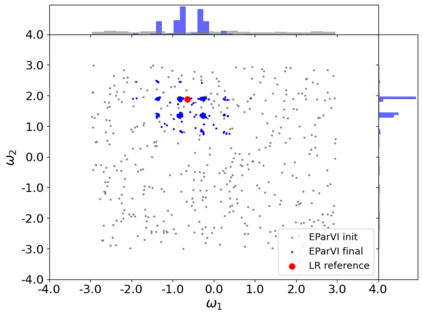
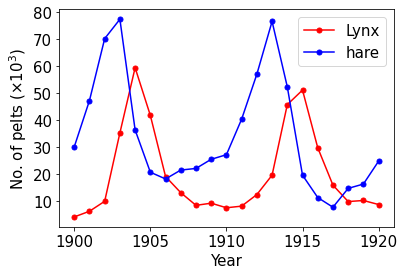
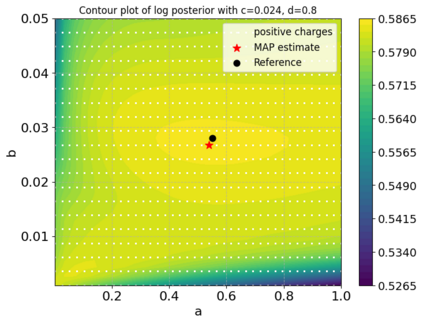
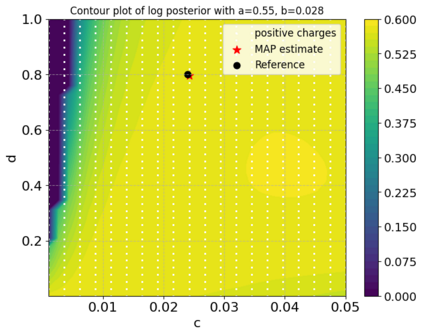
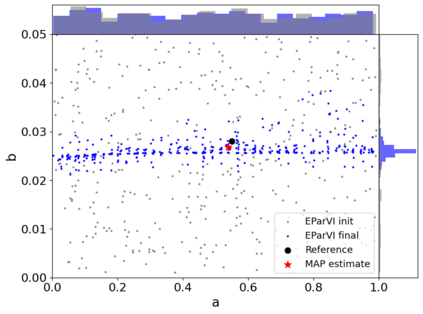
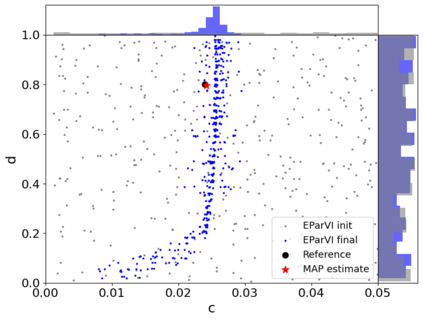
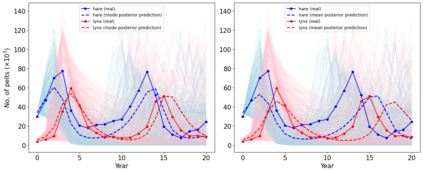
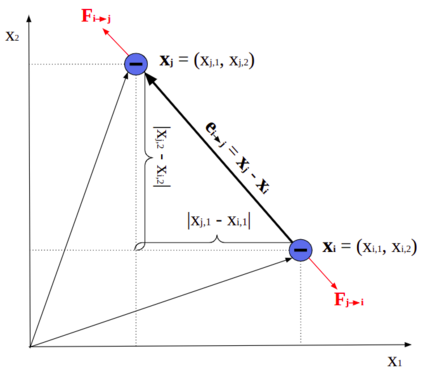
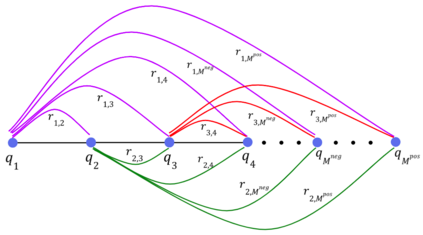
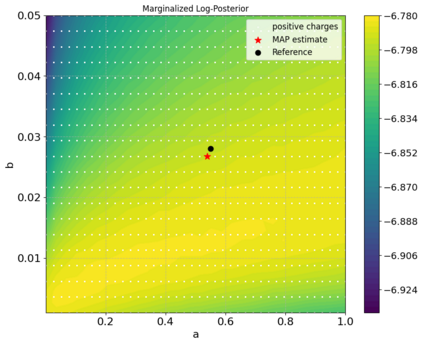
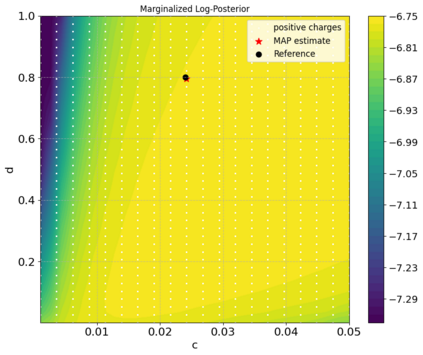
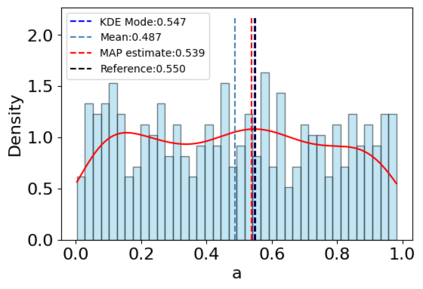
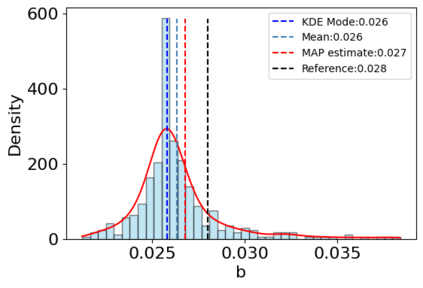
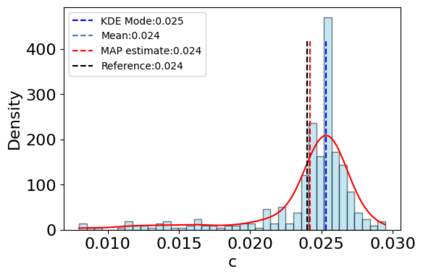
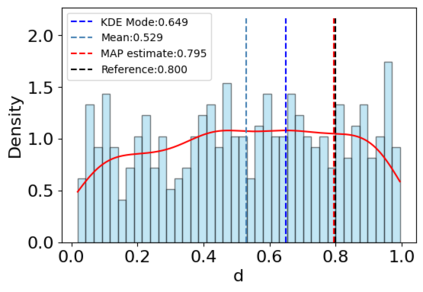
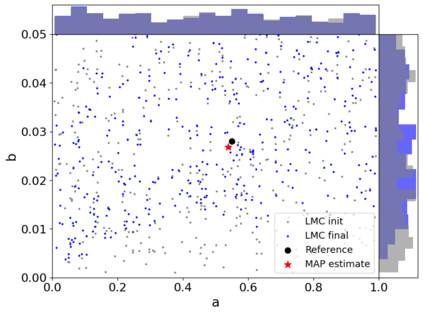
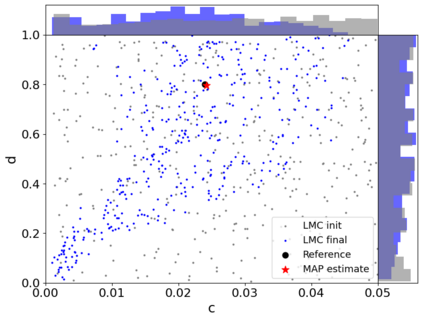
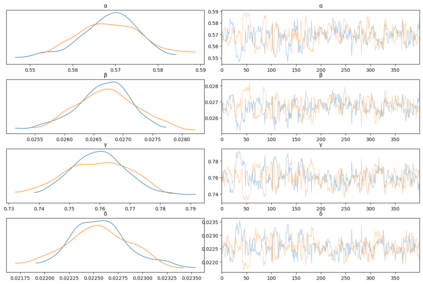
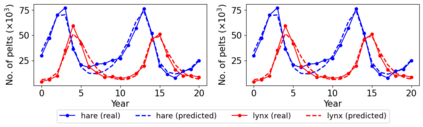
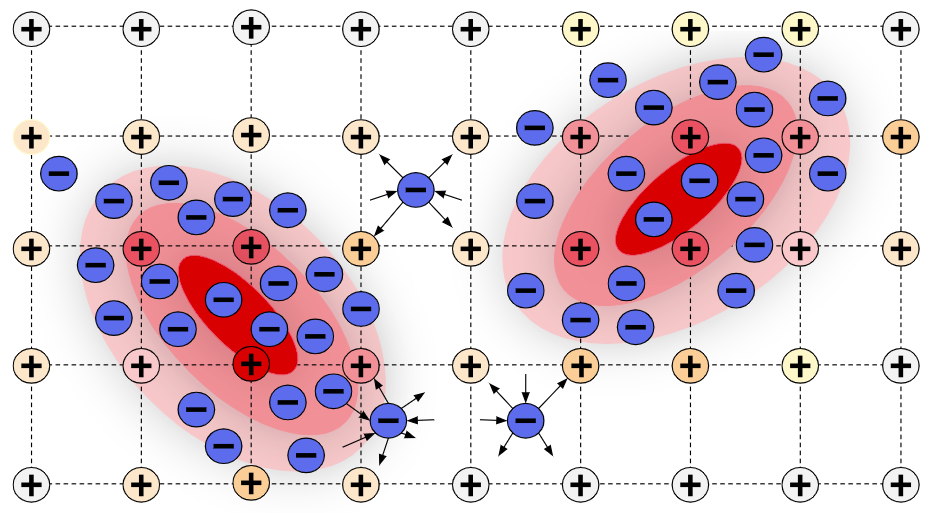
A new particle-based sampling and approximate inference method, based on electrostatics and Newton mechanics principles, is introduced with theoretical ground, algorithm design and experimental validation. This method simulates an interacting particle system (IPS) where particles, i.e. the freely-moving negative charges and spatially-fixed positive charges with magnitudes proportional to the target distribution, interact with each other via attraction and repulsion induced by the resulting electric fields described by Poisson's equation. The IPS evolves towards a steady-state where the distribution of negative charges conforms to the target distribution. This physics-inspired method offers deterministic, gradient-free sampling and inference, achieving comparable performance as other particle-based and MCMC methods in benchmark tasks of inferring complex densities, Bayesian logistic regression and dynamical system identification. A discrete-time, discrete-space algorithmic design, readily extendable to continuous time and space, is provided for usage in more general inference problems occurring in probabilistic machine learning scenarios such as Bayesian inference, generative modelling, and beyond.
翻译:暂无翻译