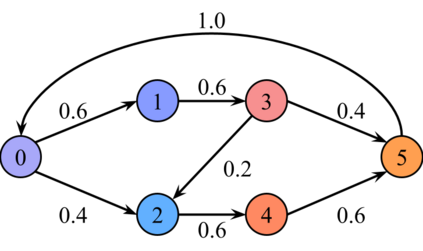
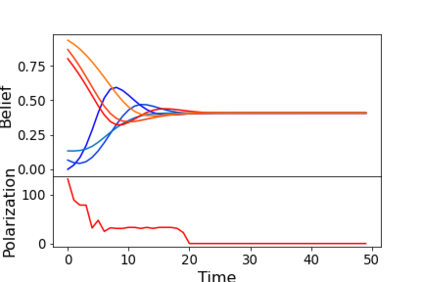
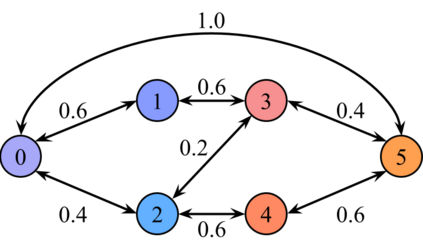
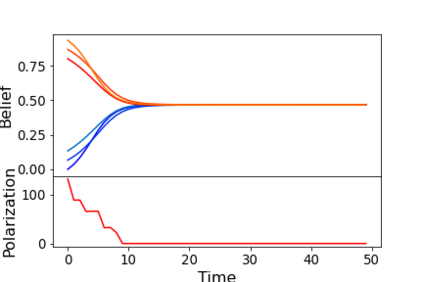
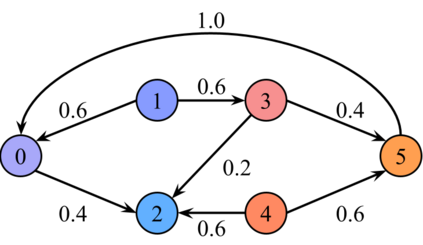
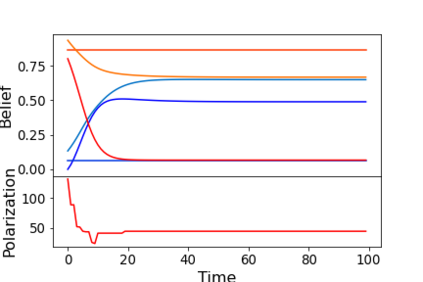
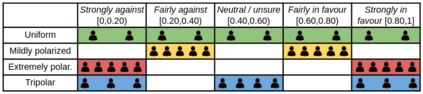
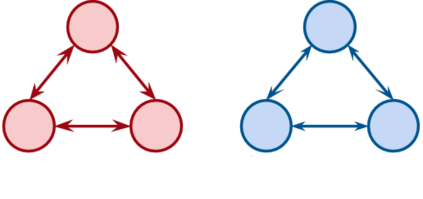
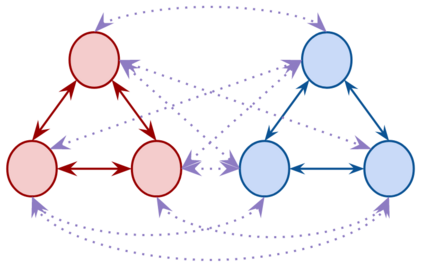
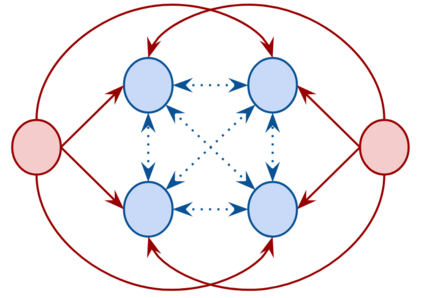
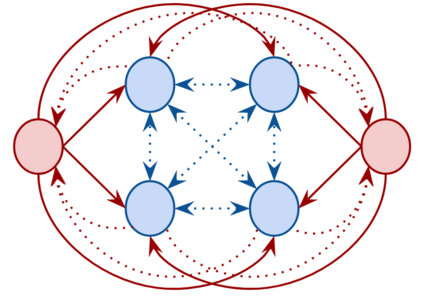
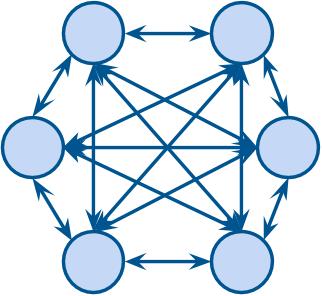
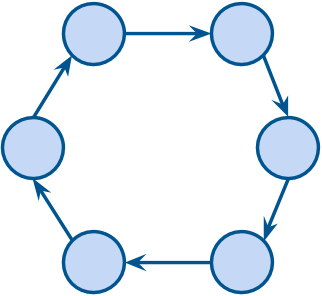
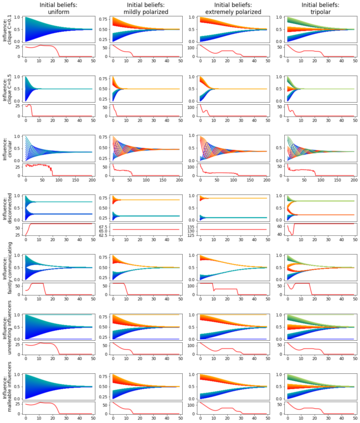
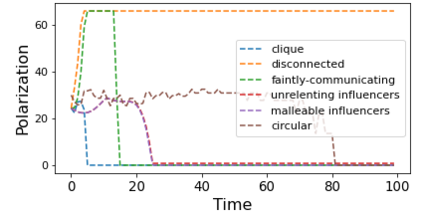
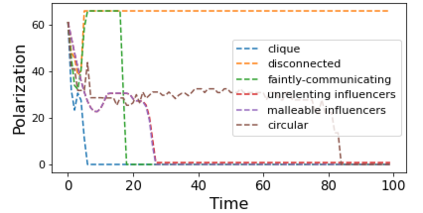
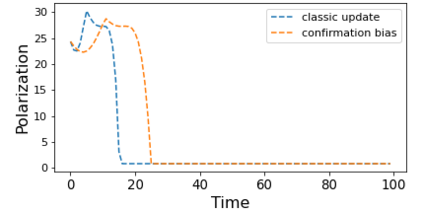
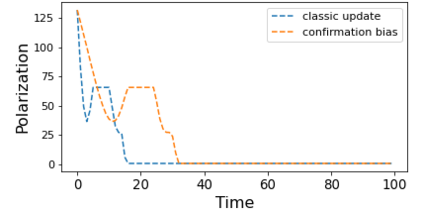
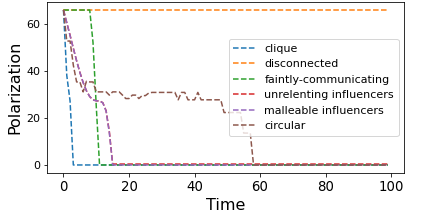
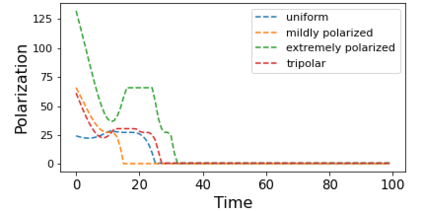
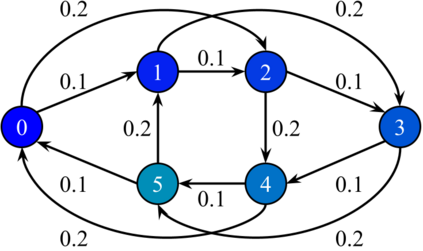
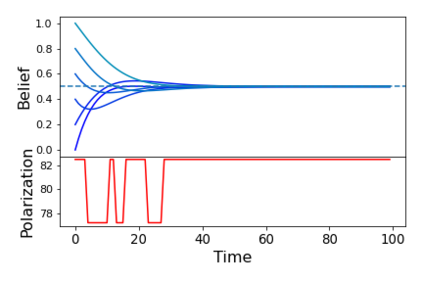
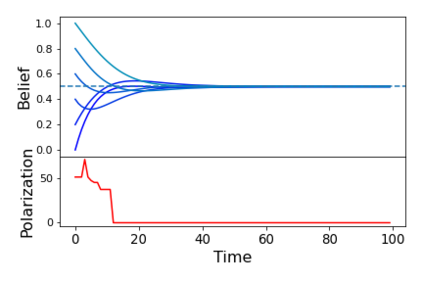
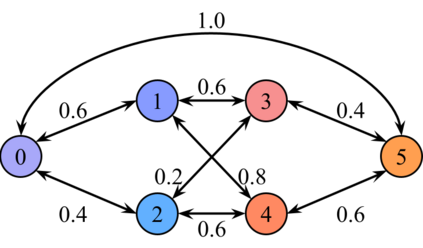
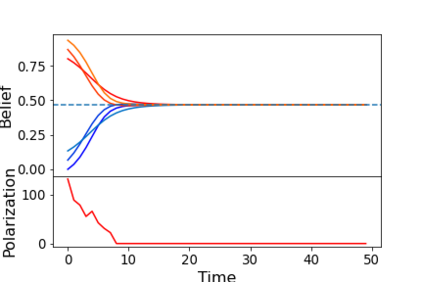
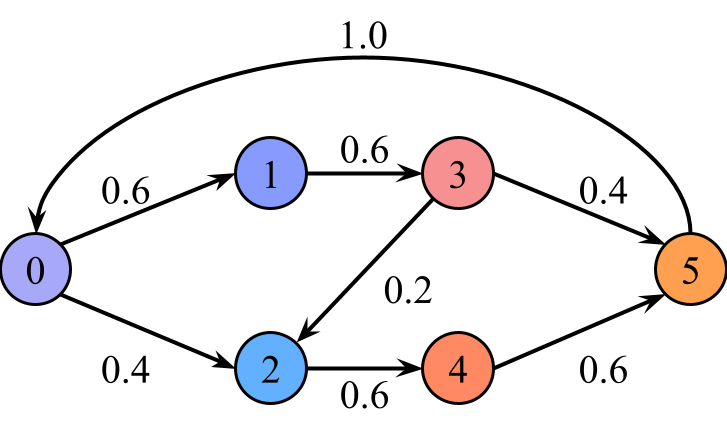
We describe a model for polarization in multi-agent systems based on Esteban and Ray's standard family of polarization measures from economics. Agents evolve by updating their beliefs (opinions) based on an underlying influence graph, as in the standard DeGroot model for social learning, but under a confirmation bias; i.e., a discounting of opinions of agents with dissimilar views. We show that even under this bias polarization eventually vanishes (converges to zero) if the influence graph is strongly-connected. If the influence graph is a regular symmetric circulation, we determine the unique belief value to which all agents converge. Our more insightful result establishes that, under some natural assumptions, if polarization does not eventually vanish then either there is a disconnected subgroup of agents, or some agent influences others more than she is influenced. We also prove that polarization does not necessarily vanish in weakly-connected graphs under confirmation bias. Furthermore, we show how our model relates to the classic DeGroot model for social learning. We illustrate our model with several simulations of a running example about polarization over vaccines and of other case studies. The theoretical results and simulations will provide insight into the phenomenon of polarization.
翻译:我们描述一个基于Esteban和Ray标准经济分化措施体系的多试剂系统极化模式。代理商根据基本影响图更新其信仰(观点)而演化,如在标准的社会学习DeGroot模式中,根据基本影响图更新其信仰(观点),但有确认偏差;即对不同观点的代理商的意见进行折扣;我们表明,即使根据这种偏差,如果影响图具有密切联系,则极化最终也会消失(从安全到零)。如果影响图是一个定期的对称循环,我们就会确定所有代理商都聚集在一起的独特信仰价值。我们更深刻的洞察结果证明,根据一些自然假设,如果两极化最终没有消失,那么就会有一个互不相连的代理商分组,或者某些代理商对其他人的影响大于她受到的影响。我们还证明,在存在确认偏差的薄弱联系的图表中,极化不一定消失。此外,我们展示我们的模型如何与典型的DeGroot模式联系起来,我们用几个模拟模型来说明我们关于疫苗和其他案例研究正在运行的两极化的例子。理论结果和模拟将会揭示两极分化现象。