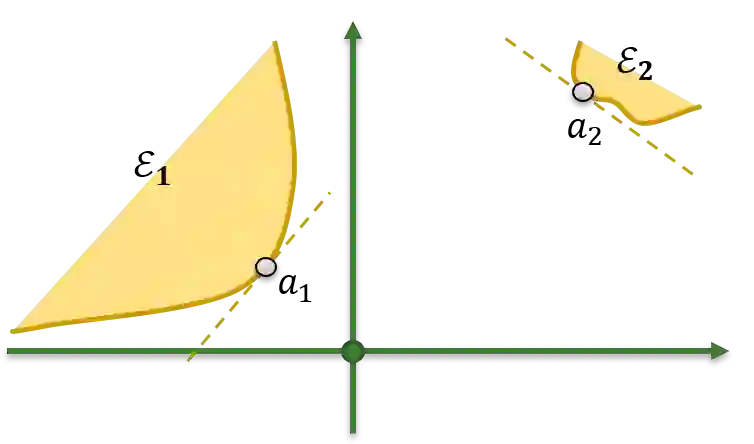
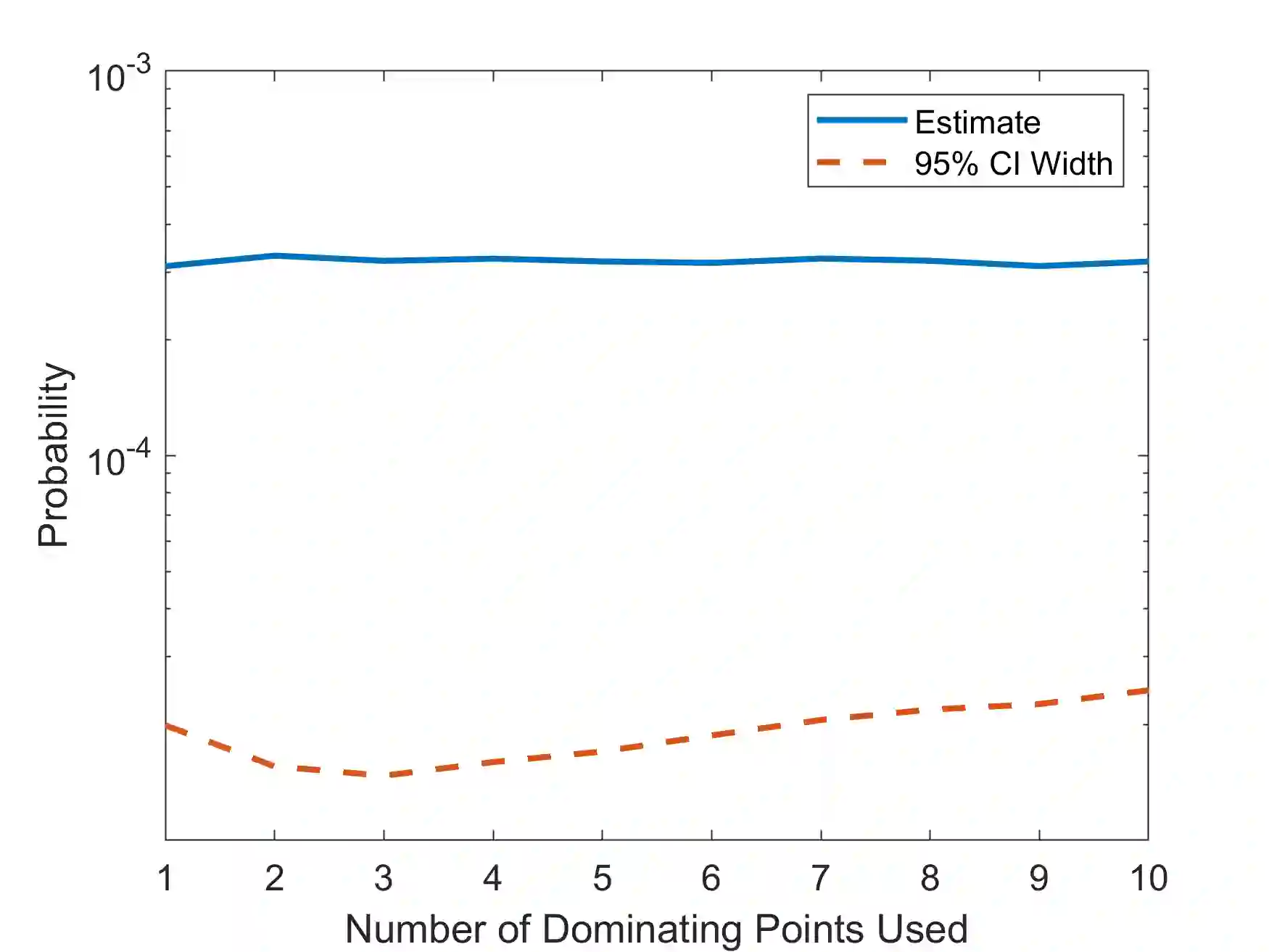
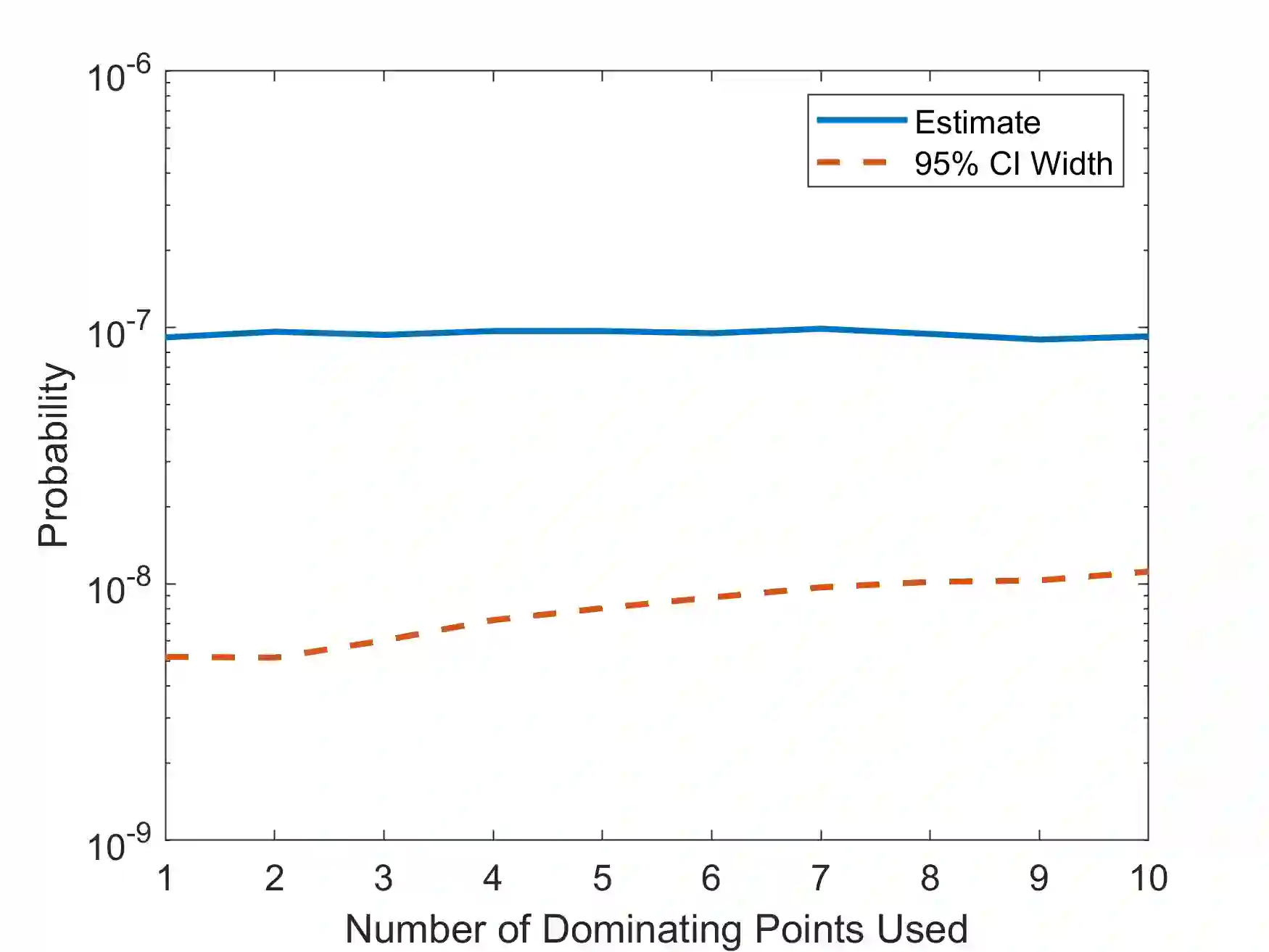
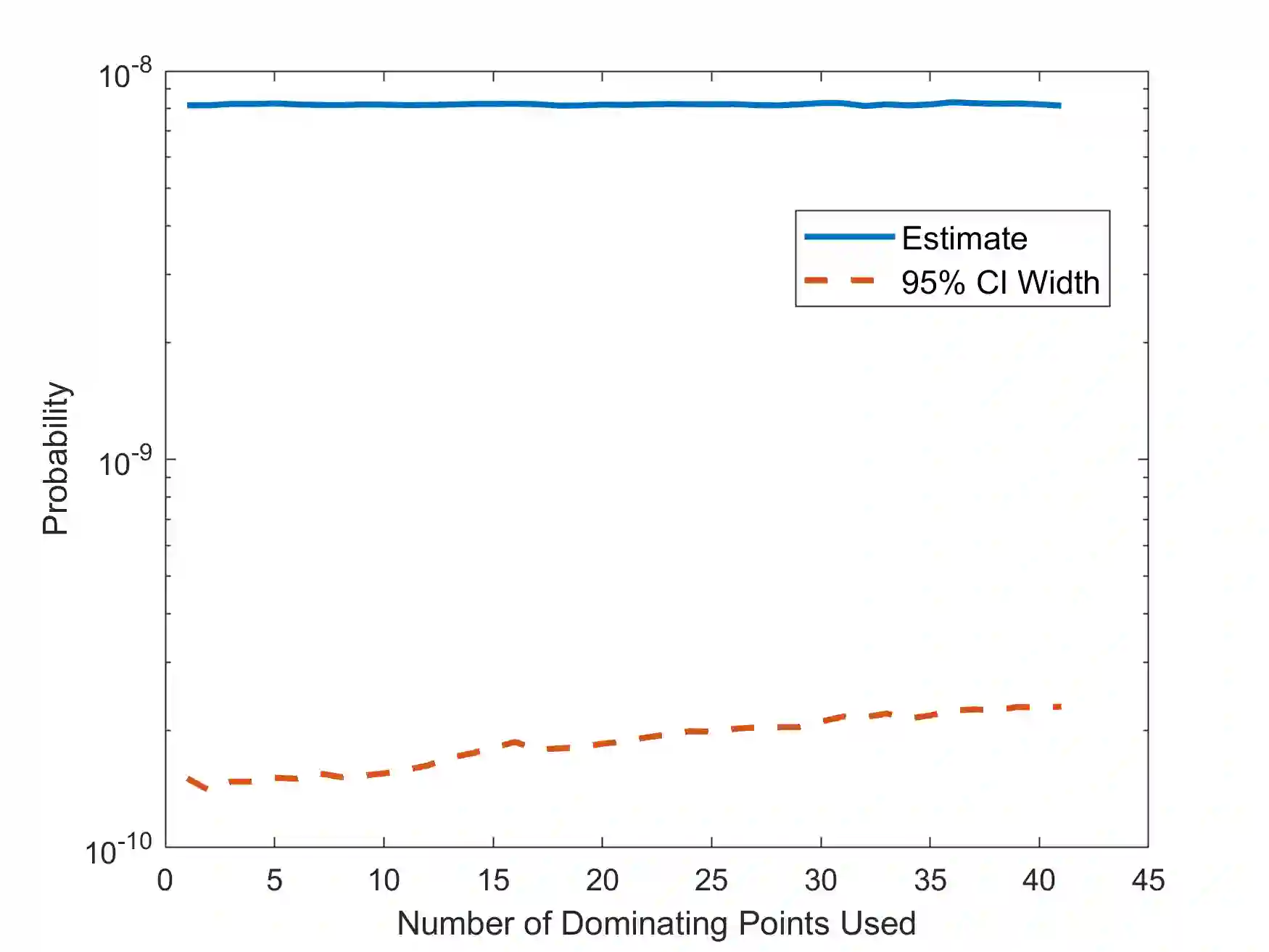
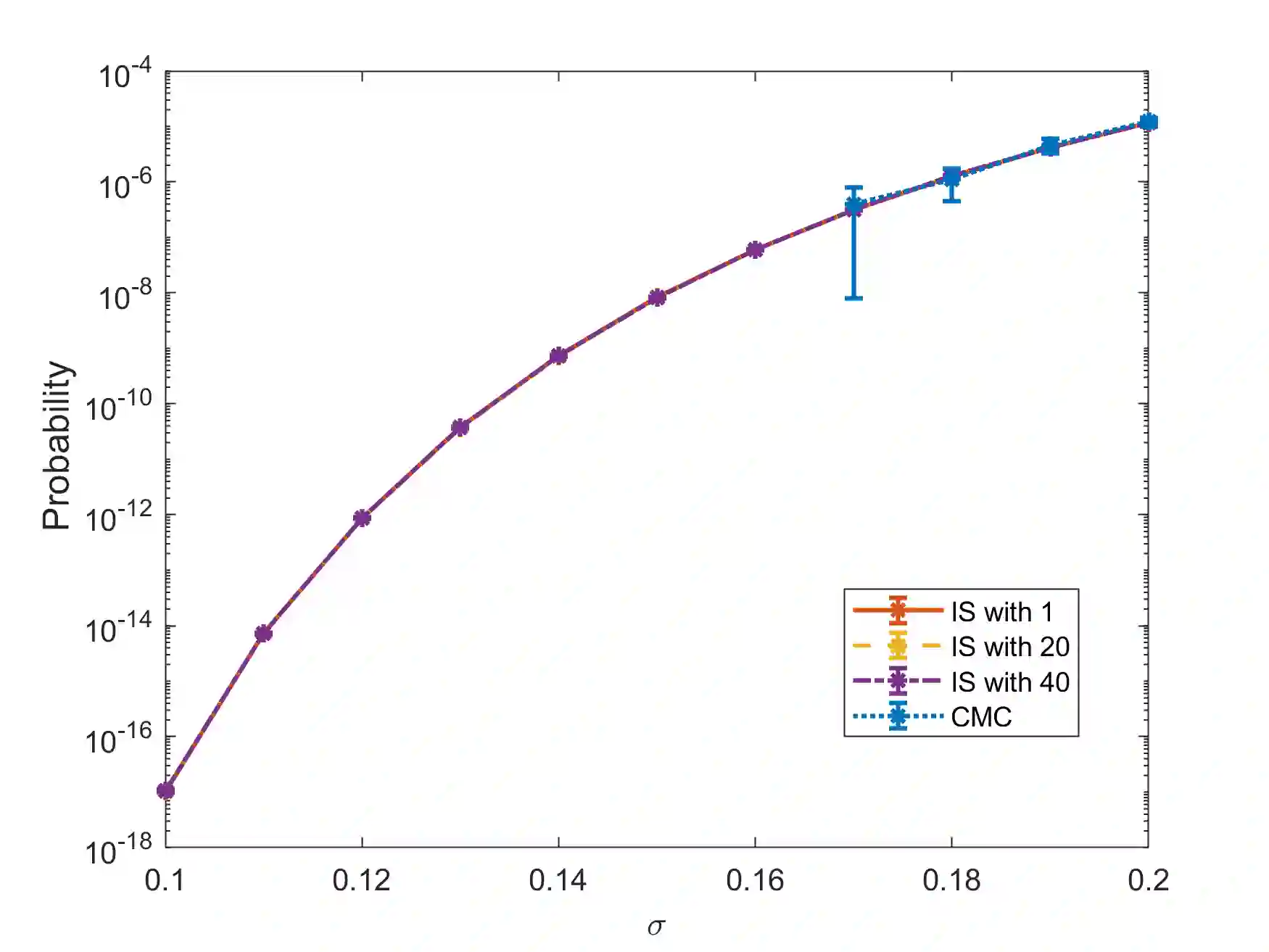
In rare-event simulation, an importance sampling (IS) estimator is regarded as efficient if its relative error, namely the ratio between its standard deviation and mean, is sufficiently controlled. It is widely known that when a rare-event set contains multiple "important regions" encoded by the so-called dominating points, IS needs to account for all of them via mixing to achieve efficiency. We argue that in typical experiments, missing less significant dominating points may not necessarily cause inefficiency, and the traditional analysis recipe could suffer from intrinsic looseness by using relative error, or in turn estimation variance, as an efficiency criterion. We propose a new efficiency notion, which we call probabilistic efficiency, to tighten this gap. In particular, we show that under the standard Gartner-Ellis large deviations regime, an IS that uses only the most significant dominating points is sufficient to attain this efficiency notion. Our finding is especially relevant in high-dimensional settings where the computational effort to locate all dominating points is enormous.
翻译:在稀有活动模拟中,如果其相对错误,即标准偏差与平均值之比之比得到充分控制,则重要抽样(IS)估计值被视为有效。众所周知,当稀有活动集包含由所谓的主导点编码的多个“重要区域”时,IS需要通过混合对所有区域负责,以实现效率。我们争辩说,在典型实验中,缺少较不重要的主导点不一定导致效率低下,传统分析配方可能因内在的松散而受损,因为使用相对错误,或反过来估计差异,作为一种效率标准。我们提出了一个新的效率概念,我们称之为概率效率,以缩小这一差距。我们特别表明,在标准的Gartner-Ellis大偏差制度下,仅使用最显著的主导点就足以实现效率概念。我们发现,在高维度环境中,确定所有主导点的计算努力是巨大的。