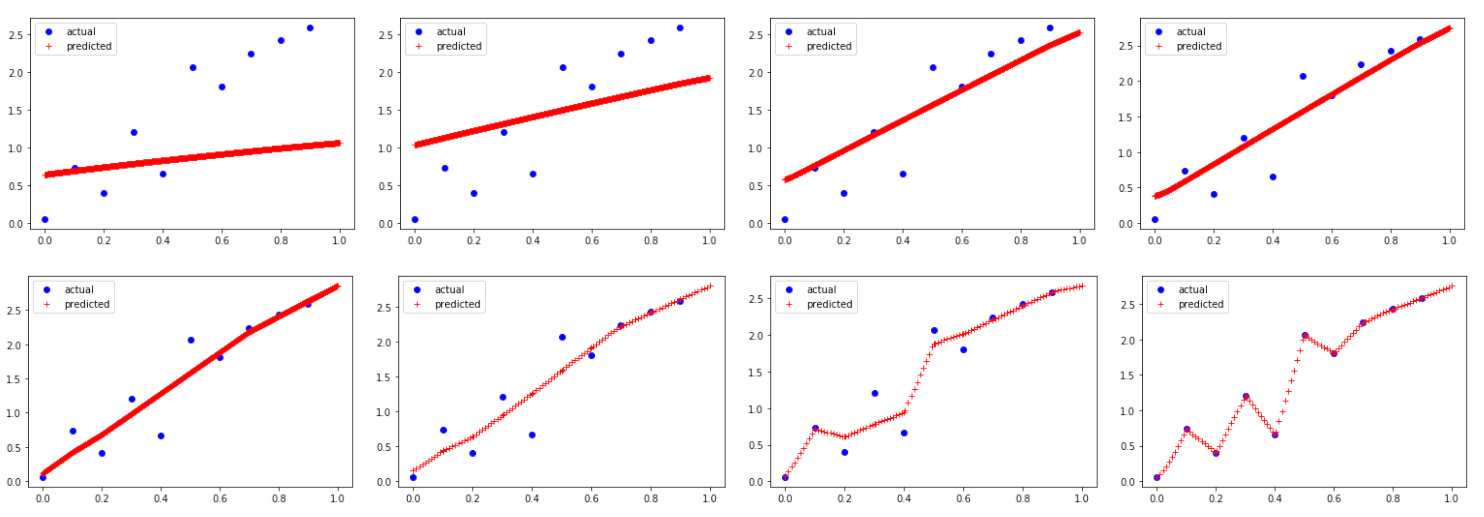
In over-parameterized deep neural networks there can be many possible parameter configurations that fit the training data exactly. However, the properties of these interpolating solutions are poorly understood. We argue that over-parameterized neural networks trained with stochastic gradient descent are subject to a Geometric Occam's Razor; that is, these networks are implicitly regularized by the geometric model complexity. For one-dimensional regression, the geometric model complexity is simply given by the arc length of the function. For higher-dimensional settings, the geometric model complexity depends on the Dirichlet energy of the function. We explore the relationship between this Geometric Occam's Razor, the Dirichlet energy and other known forms of implicit regularization. Finally, for ResNets trained on CIFAR-10, we observe that Dirichlet energy measurements are consistent with the action of this implicit Geometric Occam's Razor.
翻译:在超参数深度神经网络中,可能有许多与培训数据完全相符的参数配置。然而,这些内插解决方案的特性不甚清楚。我们争辩说,受过随机梯度梯度下降训练的超参数神经网络受几何 Occam Razor 的制约;也就是说,这些网络被几何模型复杂程度暗含了常规化。对于一维回归而言,几何模型复杂程度只是由函数的弧长度给出的。对于高维环境而言,几何模型复杂程度取决于函数的二极分光能量。我们探索了这一几何 Occam 的 Razor 、 dirichlet 能量和其他已知的隐含正规化形式之间的关系。最后,对于受过CIFAR-10 培训的ResNet,我们观察到,Drichlet 能源测量与这一隐含的几何 Occam Razor 的动作是一致的。