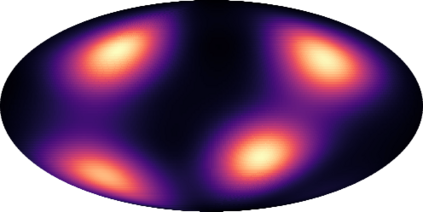
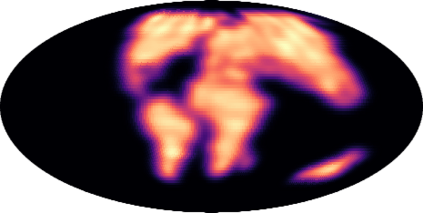
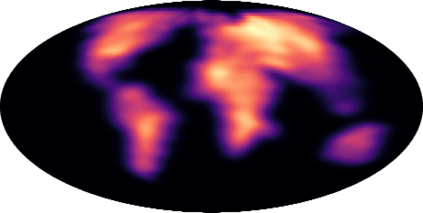
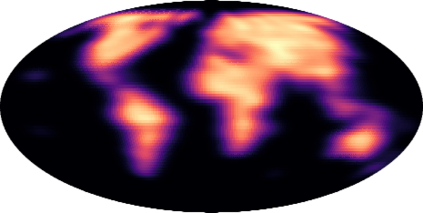
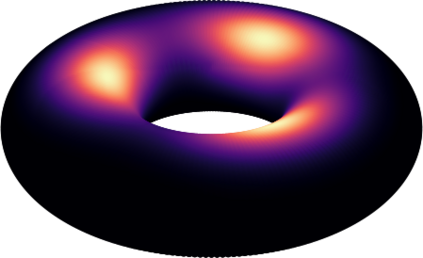
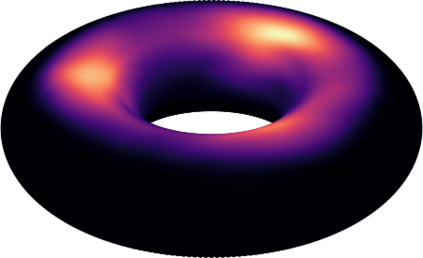
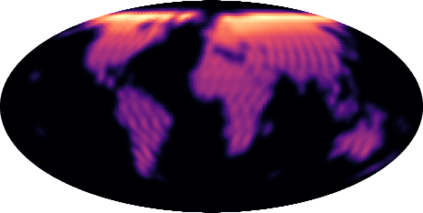
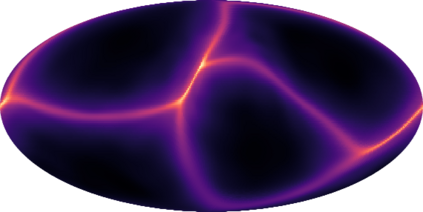
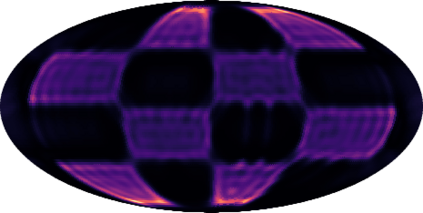
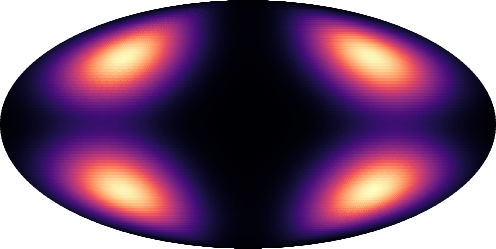
Modeling distributions on Riemannian manifolds is a crucial component in understanding non-Euclidean data that arises, e.g., in physics and geology. The budding approaches in this space are limited by representational and computational tradeoffs. We propose and study a class of flows that uses convex potentials from Riemannian optimal transport. These are universal and can model distributions on any compact Riemannian manifold without requiring domain knowledge of the manifold to be integrated into the architecture. We demonstrate that these flows can model standard distributions on spheres, and tori, on synthetic and geological data. Our source code is freely available online at http://github.com/facebookresearch/rcpm
翻译:建模在里曼尼方块上的分布是了解非欧裔数据(例如在物理学和地质学中产生的非欧裔数据)的一个关键组成部分。这个空间的起始方法受到代表性和计算性权衡的限制。我们提出并研究使用里曼尼最佳运输的锥形潜力的一类流动。这些是普遍性的,可以建模在任何紧凑的里曼尼方块上的分布,而不必要求将关于该方块的域知识纳入建筑。我们证明这些流可以建模在球体上的标准分布和关于合成和地质数据的托里标准分布。我们的源代码可以在http://github.com/facebookresearch/rcpm上自由查阅。我们的来源代码可以在http://github.com/facebookresearch/rcpm上自由查阅。