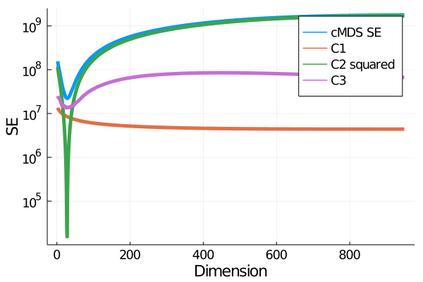
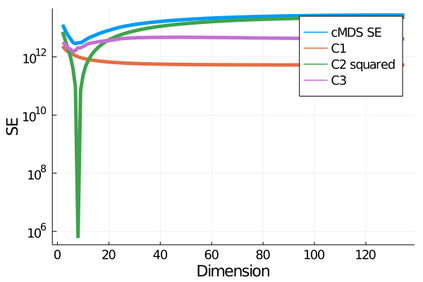
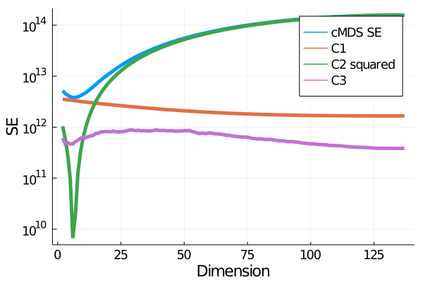
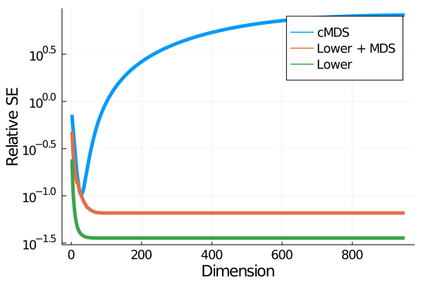
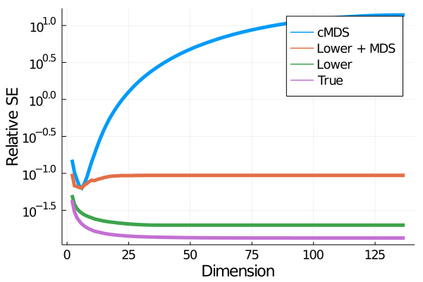
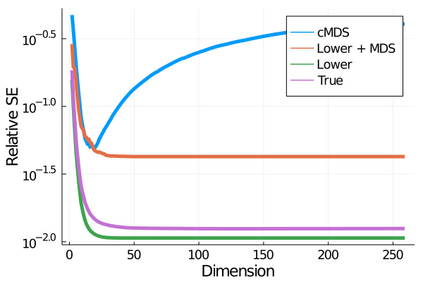
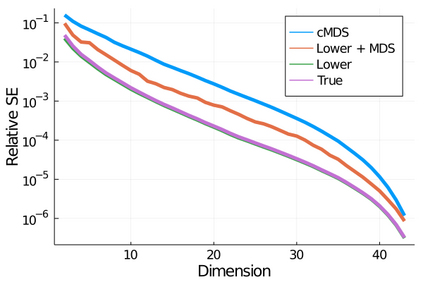
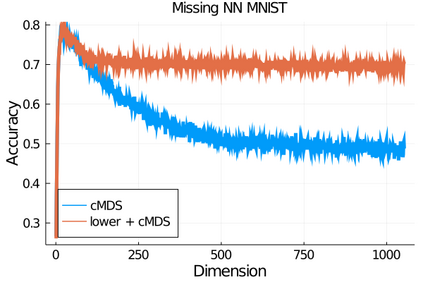
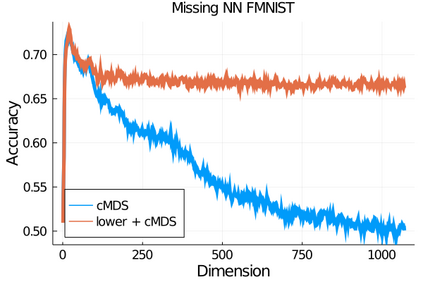
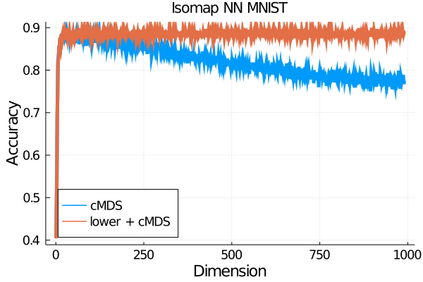
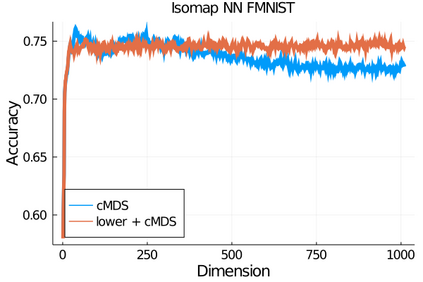
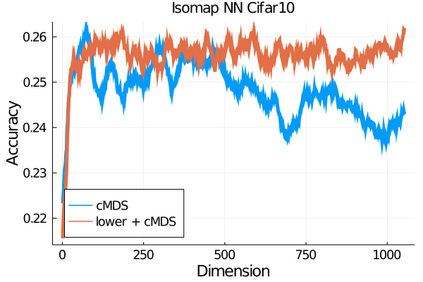
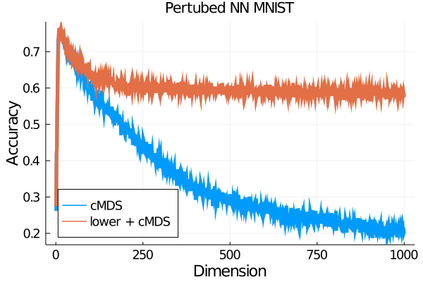
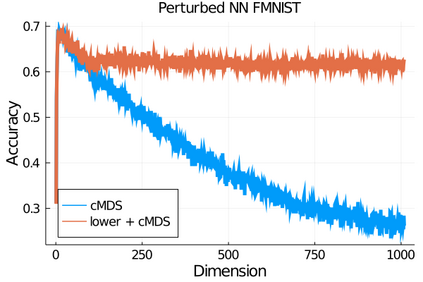
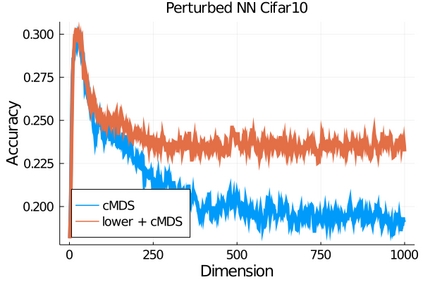
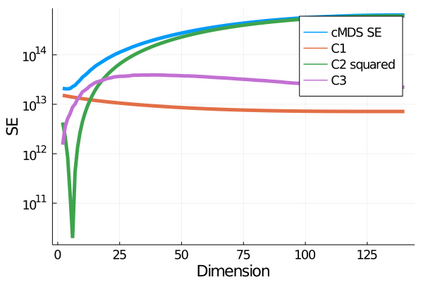
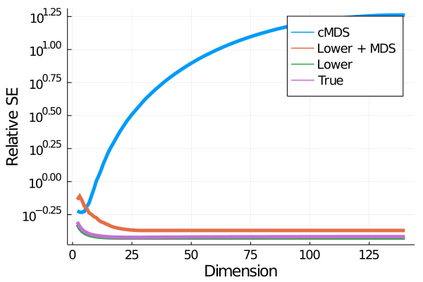
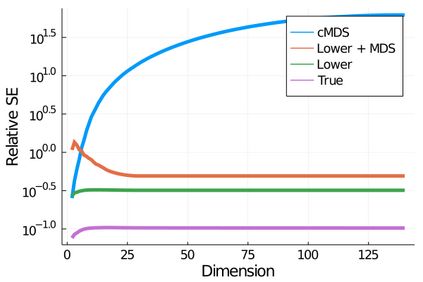
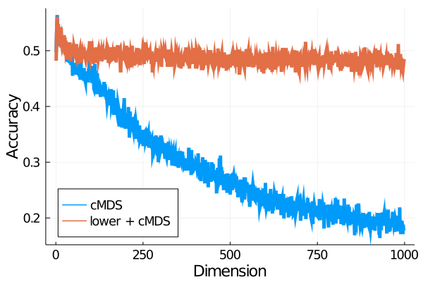
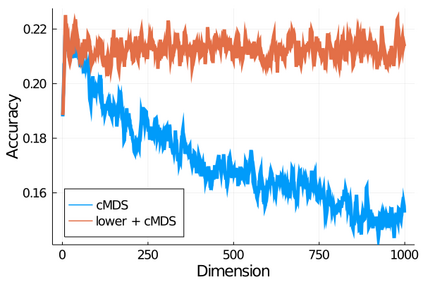
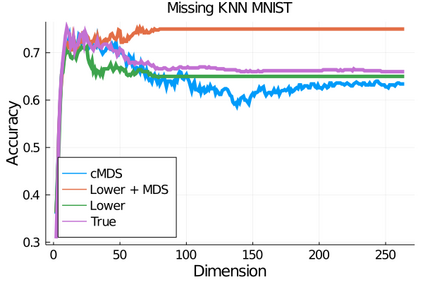
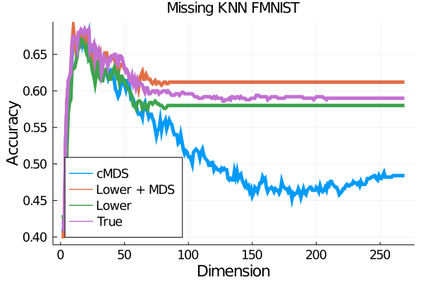
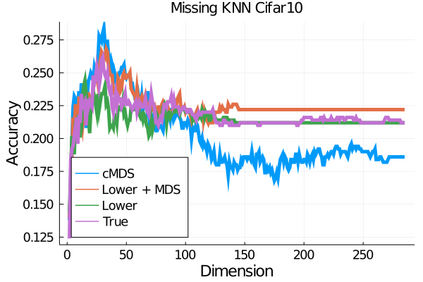
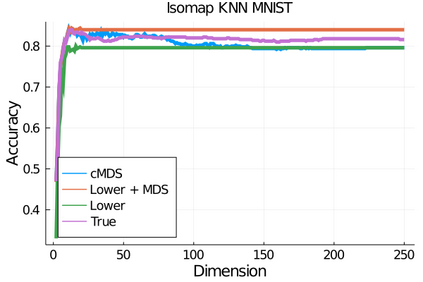
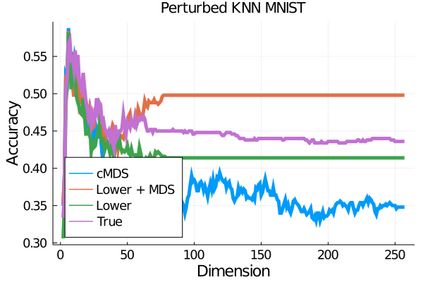
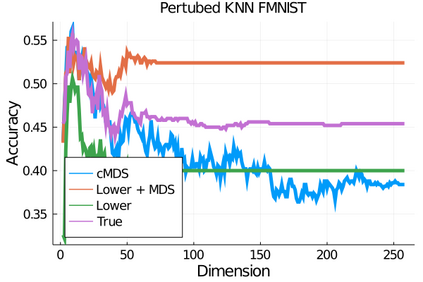
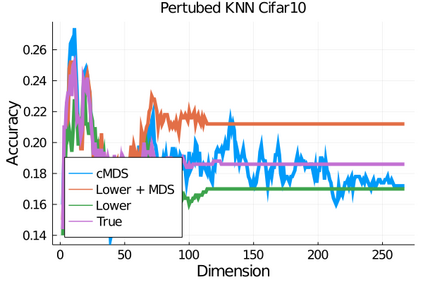
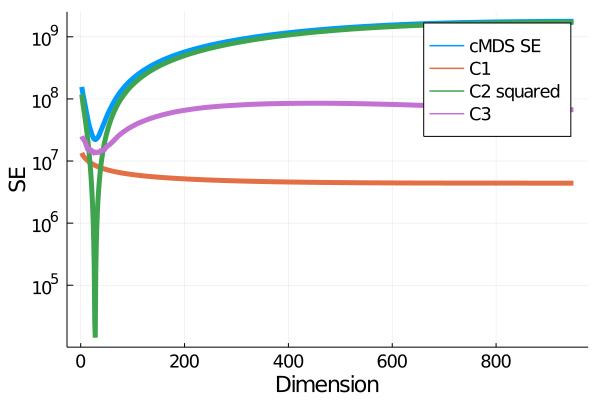
Given a matrix $D$ describing the pairwise dissimilarities of a data set, a common task is to embed the data points into Euclidean space. The classical multidimensional scaling (cMDS) algorithm is a widespread method to do this. However, theoretical analysis of the robustness of the algorithm and an in-depth analysis of its performance on non-Euclidean metrics is lacking. In this paper, we derive a formula, based on the eigenvalues of a matrix obtained from $D$, for the Frobenius norm of the difference between $D$ and the metric $D_{\text{cmds}}$ returned by cMDS. This error analysis leads us to the conclusion that when the derived matrix has a significant number of negative eigenvalues, then $\|D-D_{\text{cmds}}\|_F$, after initially decreasing, will eventually increase as we increase the dimension. Hence, counterintuitively, the quality of the embedding degrades as we increase the dimension. We empirically verify that the Frobenius norm increases as we increase the dimension for a variety of non-Euclidean metrics. We also show on several benchmark datasets that this degradation in the embedding results in the classification accuracy of both simple (e.g., 1-nearest neighbor) and complex (e.g., multi-layer neural nets) classifiers decreasing as we increase the embedding dimension. Finally, our analysis leads us to a new efficiently computable algorithm that returns a matrix $D_l$ that is at least as close to the original distances as $D_t$ (the Euclidean metric closest in $\ell_2$ distance). While $D_l$ is not metric, when given as input to cMDS instead of $D$, it empirically results in solutions whose distance to $D$ does not increase when we increase the dimension and the classification accuracy degrades less than the cMDS solution.
翻译:用于描述数据集对称差异的矩阵 $D$, 一个共同的任务就是将数据点差数的Frobenius 标准值嵌入 Euclidean 空间。 经典的多维缩放算法( CDMS) 算法是一种很普遍的方法。 但是, 算法的稳健性以及非欧clide 指标性能的深入分析都缺乏。 在本文中, 我们根据从$D获得的矩阵的偏重值, 共同的任务是将数据点嵌入 $D 和 $$D 的调值差值。 这个错误分析让我们得出这样的结论: 当衍生的矩阵具有大量负电子值时, 那么当我们增加尺寸时, 美元D- d text{ mds_F$, 最终会增加一个公式。 因此, 相对直观地, 嵌入的特性会降低到新维度。 我们从 Frobenbinius 标准提高的值值值值值值值值值值, 当我们增加一个更近的内基化的内基值值数据时, 。