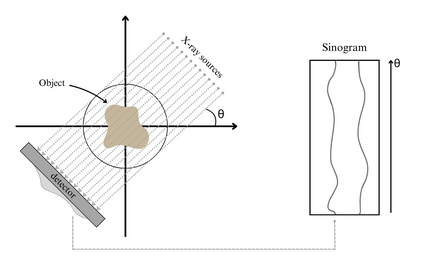
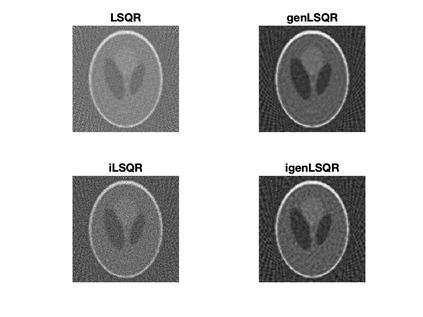
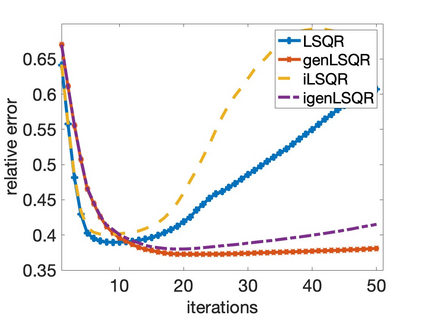
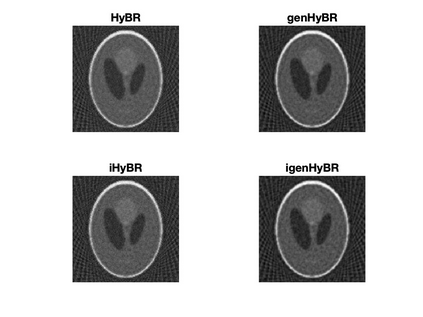
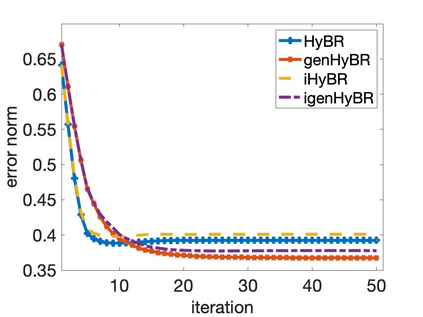
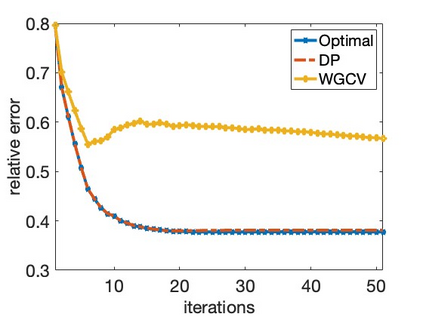
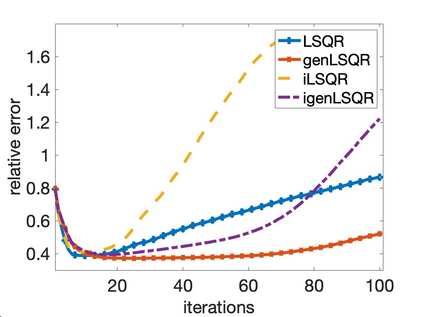
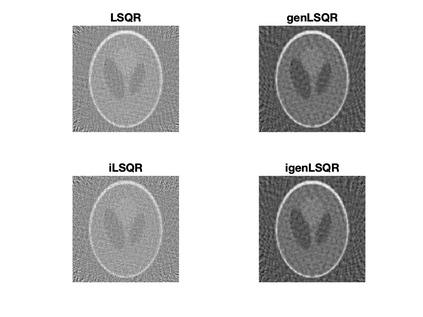
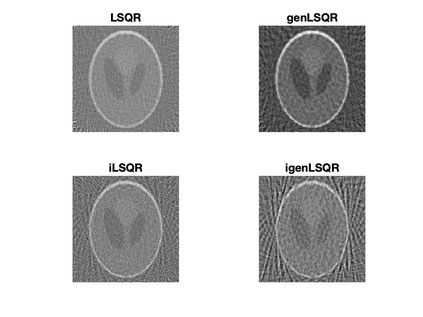
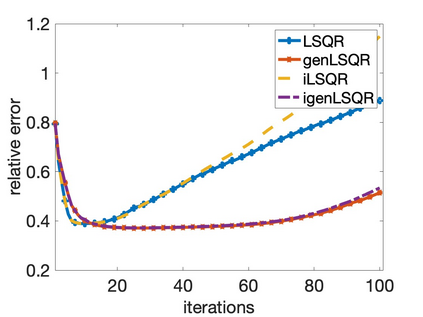
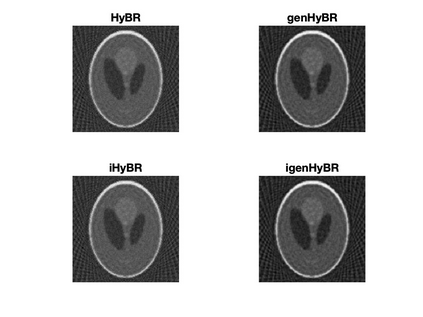
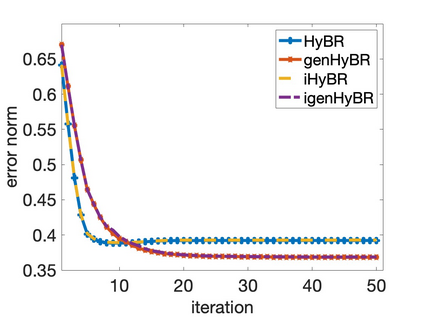
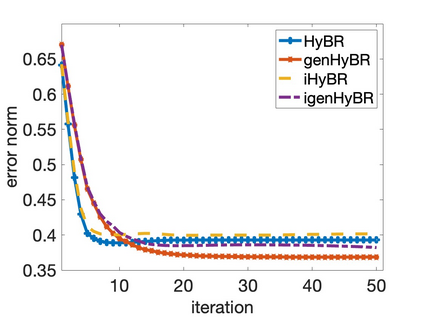
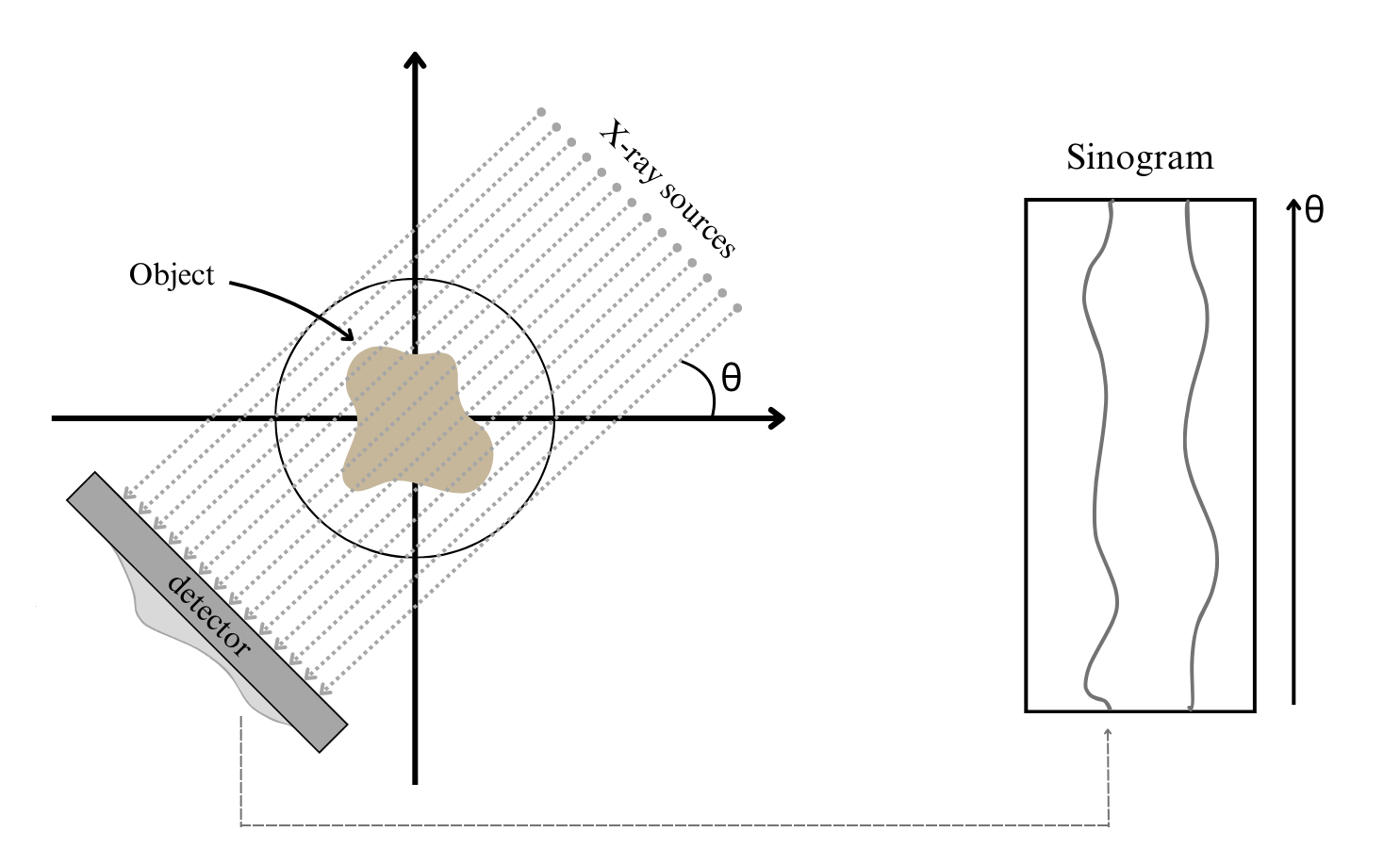
Solving large-scale Bayesian inverse problems presents significant challenges, particularly when the exact (discretized) forward operator is unavailable. These challenges often arise in image processing tasks due to unknown defects in the forward process that may result in varying degrees of inexactness in the forward model. Moreover, for many large-scale problems, computing the square root or inverse of the prior covariance matrix is infeasible such as when the covariance kernel is defined on irregular grids or is accessible only through matrix-vector products. This paper introduces an efficient approach by developing an inexact generalized Golub-Kahan decomposition that can incorporate varying degrees of inexactness in the forward model to solve large-scale generalized Tikhonov regularized problems. Further, a hybrid iterative projection scheme is developed to automatically select Tikhonov regularization parameters. Numerical experiments on simulated tomography reconstructions demonstrate the stability and effectiveness of this novel hybrid approach.
翻译:暂无翻译