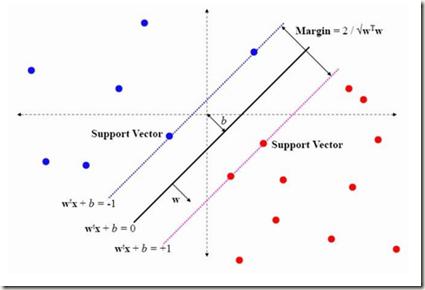
The literature on "benign overfitting" in overparameterized models has been mostly restricted to regression or binary classification; however, modern machine learning operates in the multiclass setting. Motivated by this discrepancy, we study benign overfitting in multiclass linear classification. Specifically, we consider the following training algorithms on separable data: (i) empirical risk minimization (ERM) with cross-entropy loss, which converges to the multiclass support vector machine (SVM) solution; (ii) ERM with least-squares loss, which converges to the min-norm interpolating (MNI) solution; and, (iii) the one-vs-all SVM classifier. First, we provide a simple sufficient deterministic condition under which all three algorithms lead to classifiers that interpolate the training data and have equal accuracy. When the data is generated from Gaussian mixtures or a multinomial logistic model, this condition holds under high enough effective overparameterization. We also show that this sufficient condition is satisfied under "neural collapse", a phenomenon that is observed in training deep neural networks. Second, we derive novel bounds on the accuracy of the MNI classifier, thereby showing that all three training algorithms lead to benign overfitting under sufficient overparameterization. Ultimately, our analysis shows that good generalization is possible for SVM solutions beyond the realm in which typical margin-based bounds apply.
翻译:暂无翻译