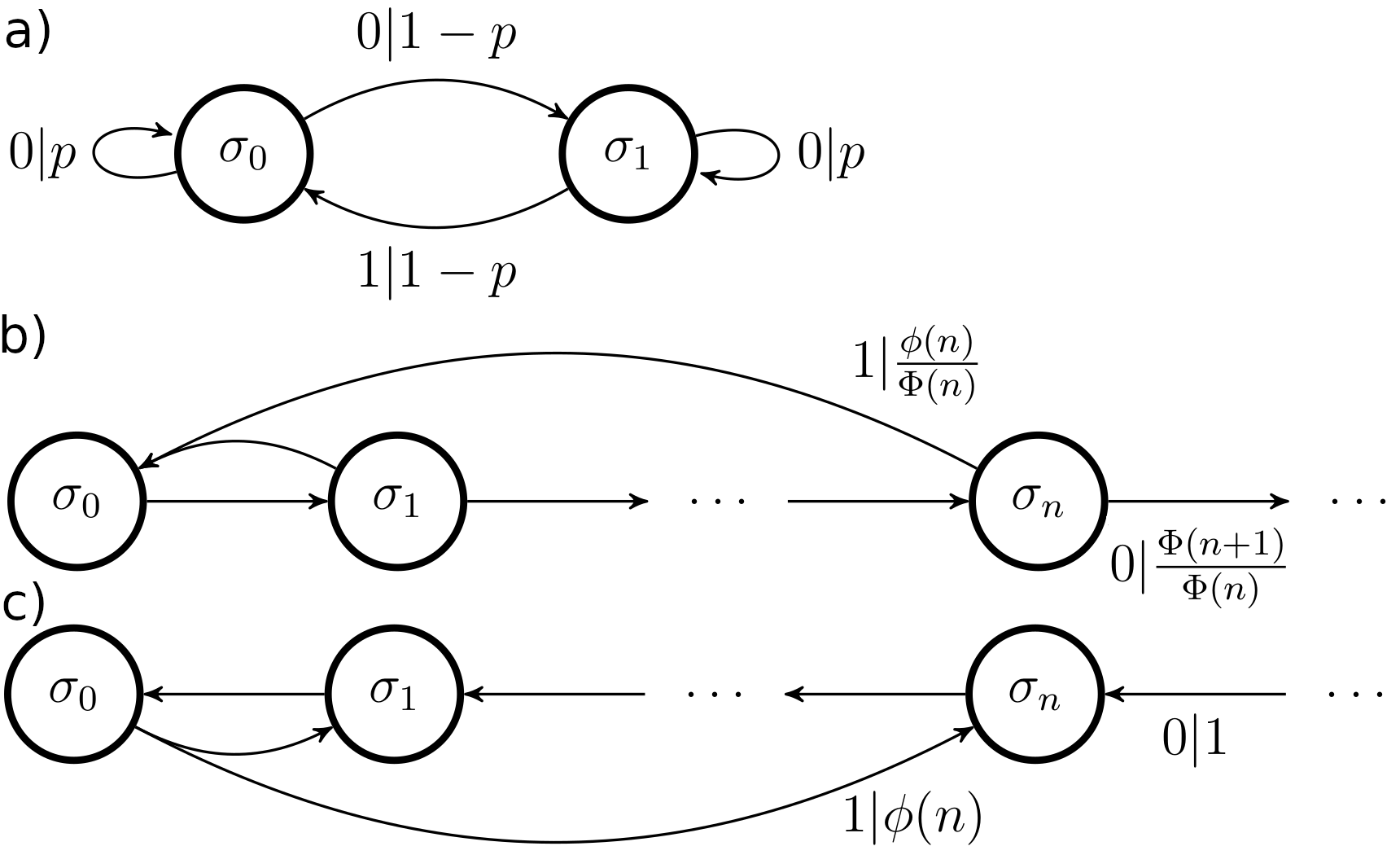
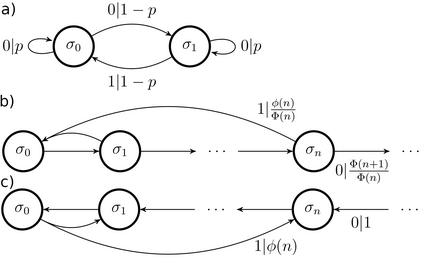
Stochastic modelling is an essential component of the quantitative sciences, with hidden Markov models (HMMs) often playing a central role. Concurrently, the rise of quantum technologies promises a host of advantages in computational problems, typically in terms of the scaling of requisite resources such as time and memory. HMMs are no exception to this, with recent results highlighting quantum implementations of deterministic HMMs exhibiting superior memory and thermal efficiency relative to their classical counterparts. In many contexts however, non-deterministic HMMs are viable alternatives; compared to them the advantages of current quantum implementations do not always hold. Here, we provide a systematic prescription for constructing quantum implementations of non-deterministic HMMs that re-establish the quantum advantages against this broader class. Crucially, we show that whenever the classical implementation suffers from thermal dissipation due to its need to process information in a time-local manner, our quantum implementations will both mitigate some of this dissipation, and achieve an advantage in memory compression.
翻译:托盘建模是定量科学的一个基本组成部分,隐藏的马尔科夫模型(MMMs)常常发挥核心作用。 同时,量子技术的崛起在计算问题方面带来许多优势,通常在时间和记忆等必要资源的扩大方面。 赫米姆斯也不例外,最近的结果突出了确定性高米的量子执行,相对于其古典同类而言,它具有较高的记忆力和热效率。 然而,在许多情况下,非确定性高米是可行的替代物;与之相比,目前量子执行的优势并不总能维持。 在这里,我们为构建非非确定性高米的量执行提供了系统性的处方,从而针对这一更广泛的类别重新建立量子优势。 很显然,我们表明,每当典型的执行由于需要按时间处理信息而出现热耗时,我们的量执行既能减轻部分的分散现象,又在记忆压缩方面获得优势。