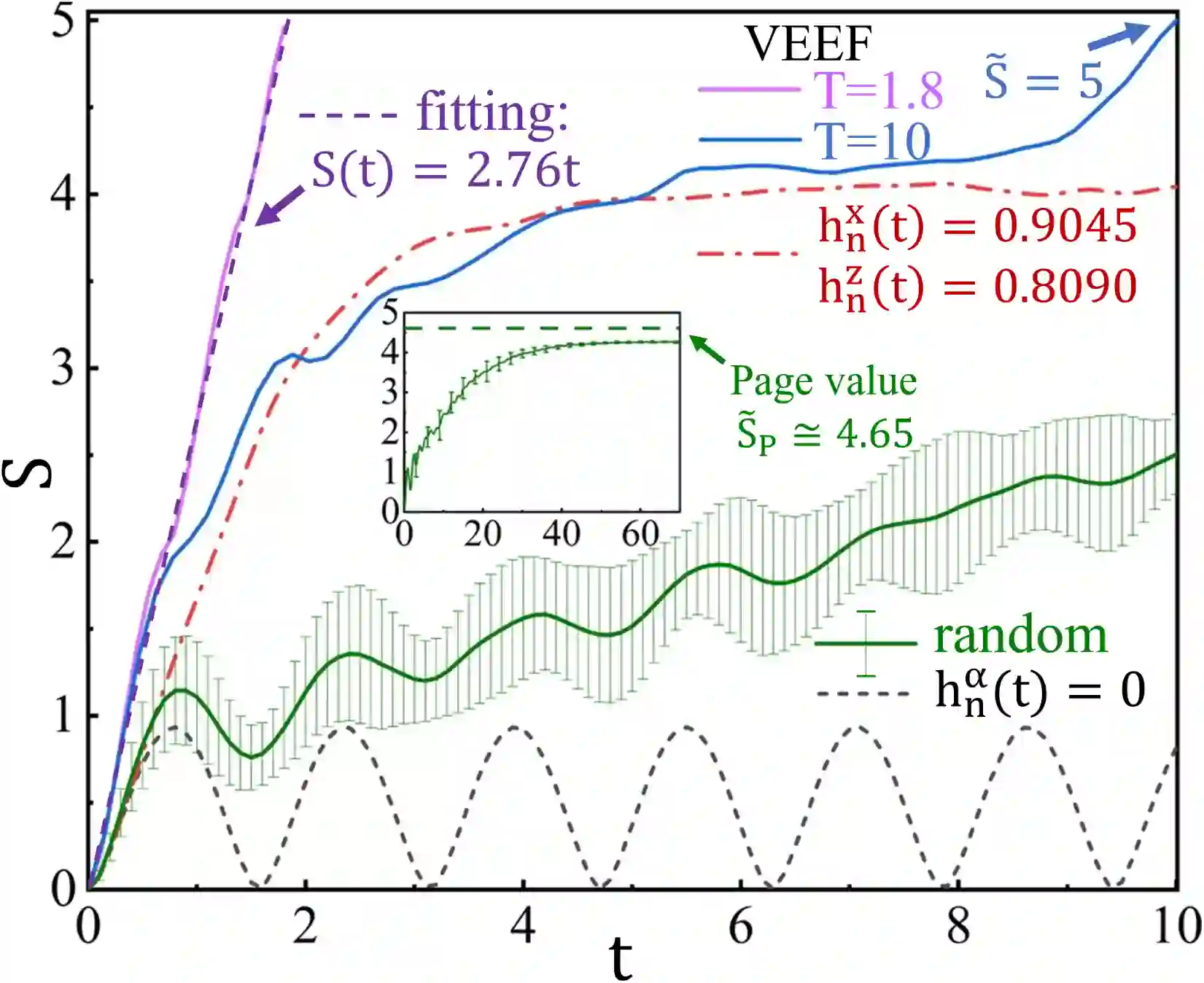
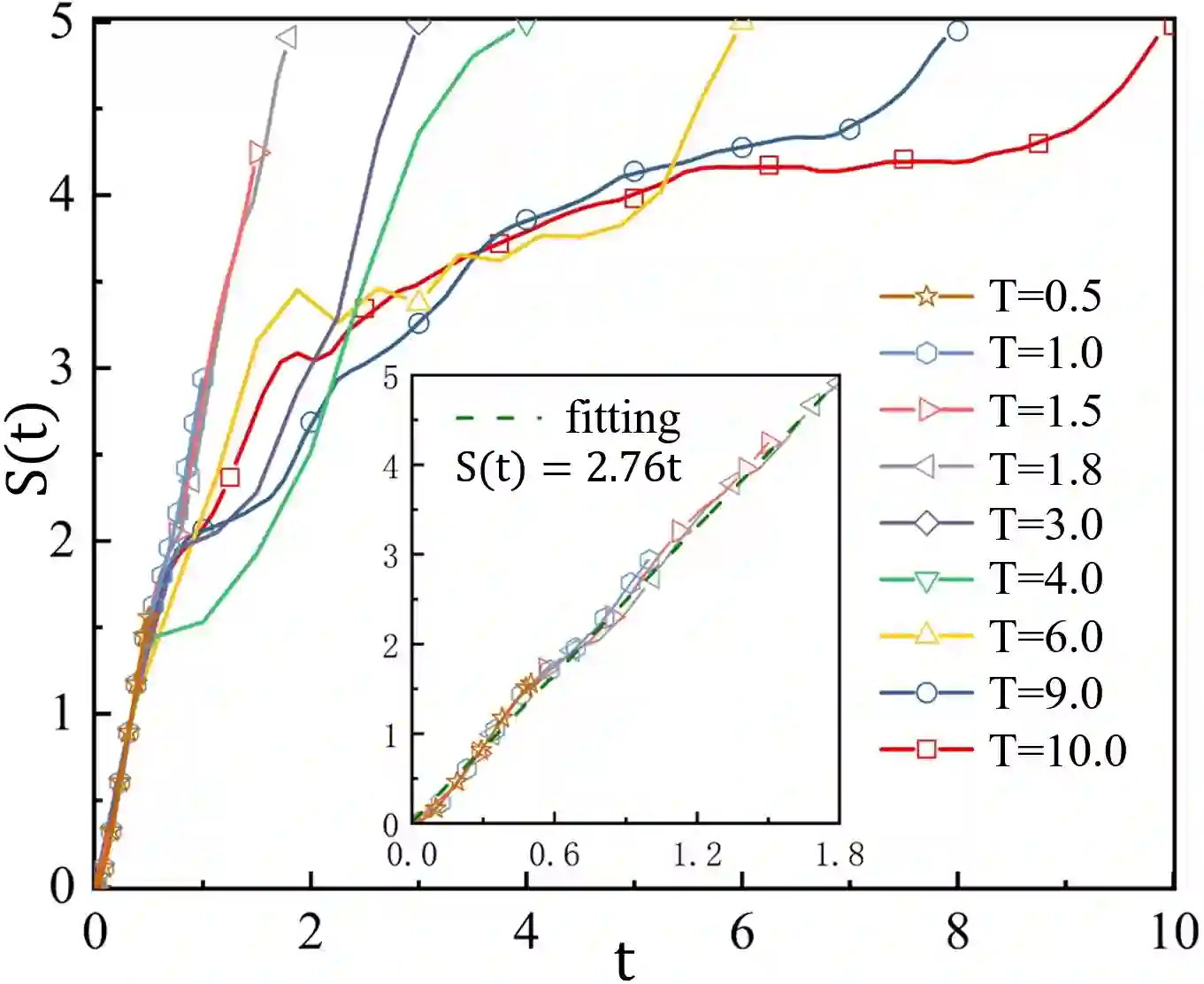
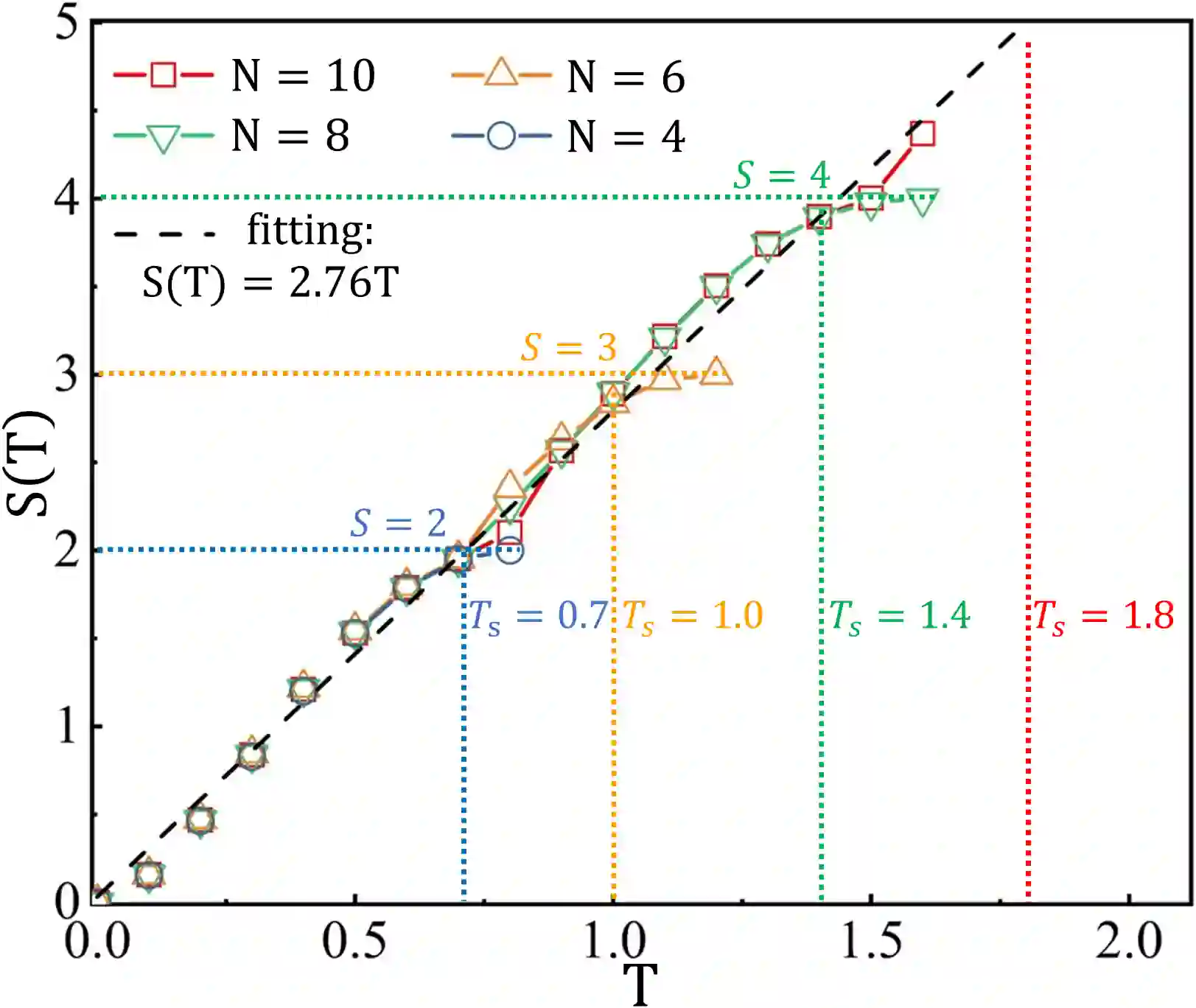
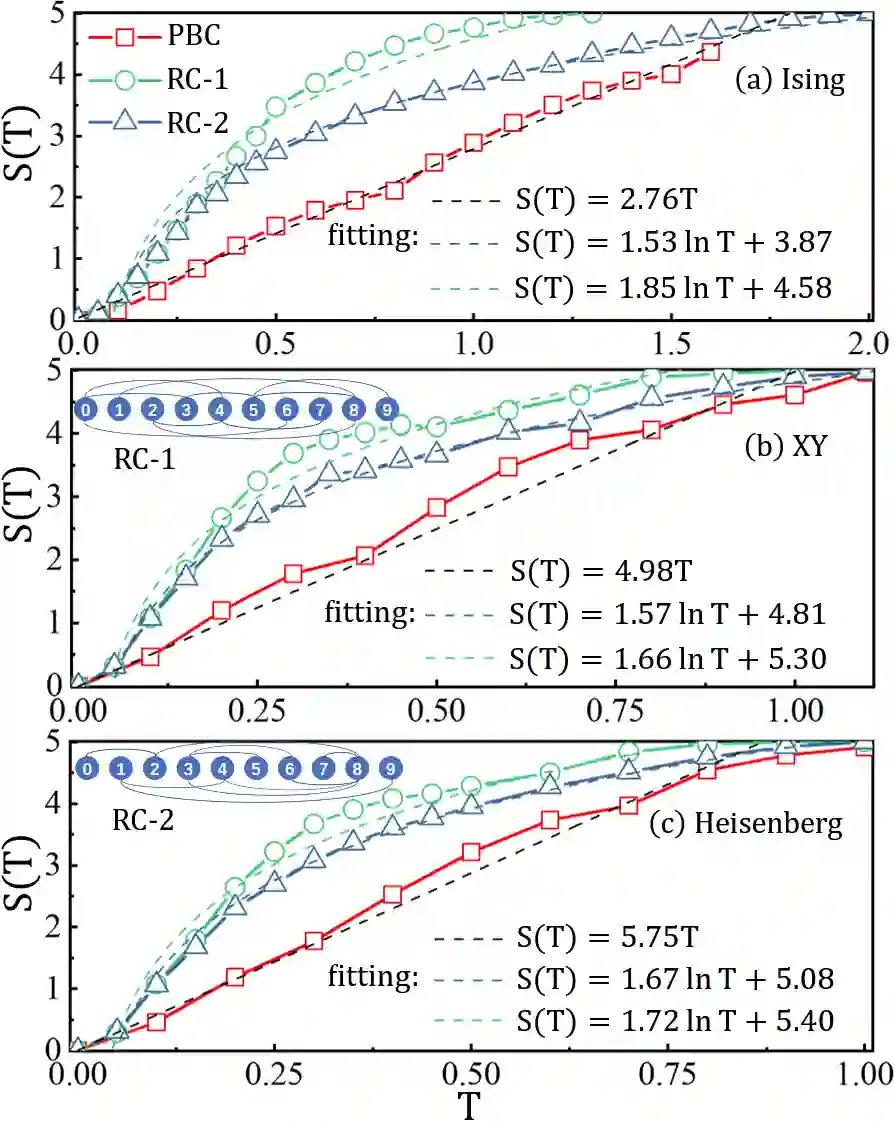
Entanglement propagation provides a key routine to understand quantum many-body dynamics in and out of equilibrium. In this work, we uncover that the ``variational entanglement-enhancing'' field (VEEF) robustly induces a persistent ballistic spreading of entanglement in quantum spin chains. The VEEF is time dependent, and is optimally controlled to maximize the bipartite entanglement entropy (EE) of the final state. Such a linear growth persists till the EE reaches the genuine saturation $\tilde{S} = - \log_{2} 2^{-\frac{N}{2}}=\frac{N}{2}$ with $N$ the total number of spins. The EE satisfies $S(t) = v t$ for the time $t \leq \frac{N}{2v}$, with $v$ the velocity. These results are in sharp contrast with the behaviors without VEEF, where the EE generally approaches a sub-saturation known as the Page value $\tilde{S}_{P} =\tilde{S} - \frac{1}{2\ln{2}}$ in the long-time limit, and the entanglement growth deviates from being linear before the Page value is reached. The dependence between the velocity and interactions is explored, with $v \simeq 2.76$, $4.98$, and $5.75$ for the spin chains with Ising, XY, and Heisenberg interactions, respectively. We further show that the nonlinear growth of EE emerges with the presence of long-range interactions.
翻译:暂无翻译