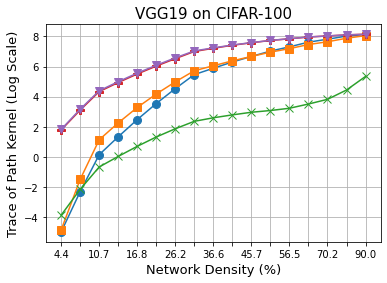
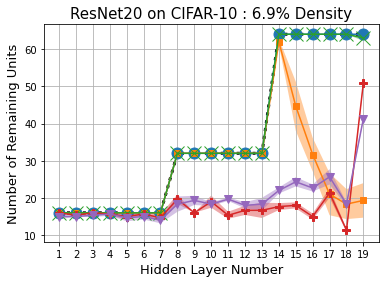
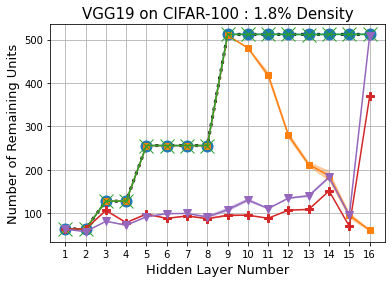
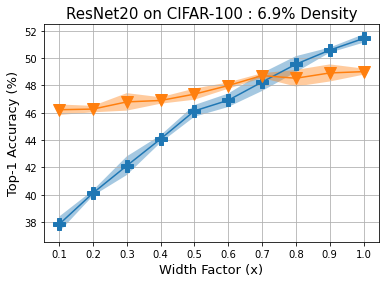
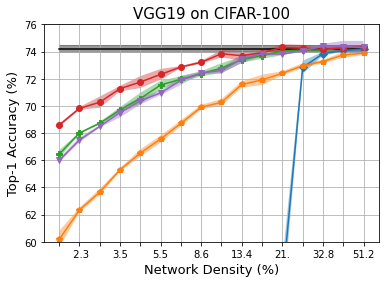
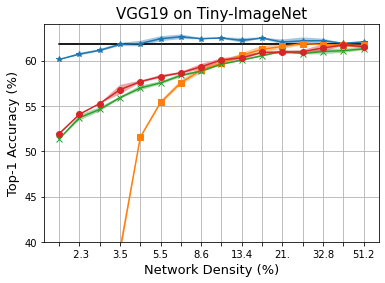
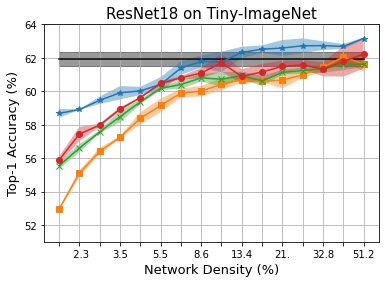
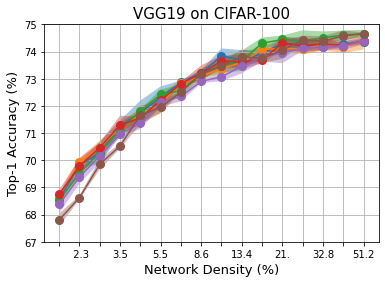
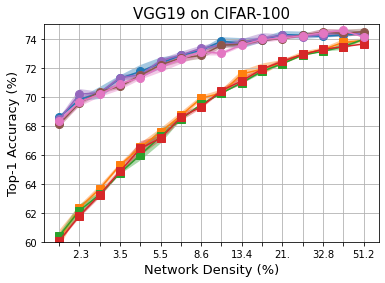
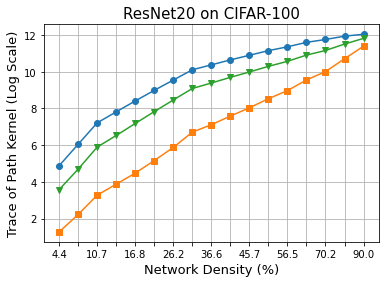
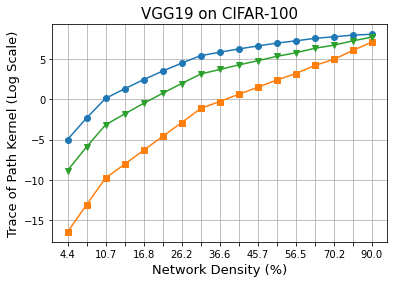
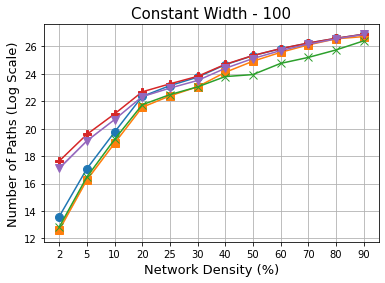
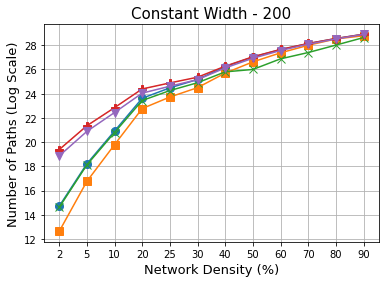
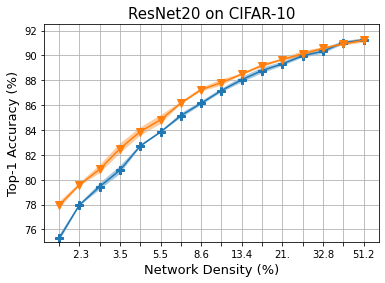
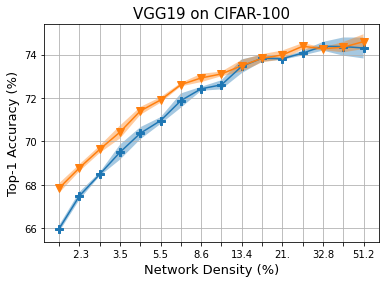
Methods that sparsify a network at initialization are important in practice because they greatly improve the efficiency of both learning and inference. Our work is based on a recently proposed decomposition of the Neural Tangent Kernel (NTK) that has decoupled the dynamics of the training process into a data-dependent component and an architecture-dependent kernel - the latter referred to as Path Kernel. That work has shown how to design sparse neural networks for faster convergence, without any training data, using the Synflow-L2 algorithm. We first show that even though Synflow-L2 is optimal in terms of convergence, for a given network density, it results in sub-networks with "bottleneck" (narrow) layers - leading to poor performance as compared to other data-agnostic methods that use the same number of parameters. Then we propose a new method to construct sparse networks, without any training data, referred to as Paths with Higher-Edge Weights (PHEW). PHEW is a probabilistic network formation method based on biased random walks that only depends on the initial weights. It has similar path kernel properties as Synflow-L2 but it generates much wider layers, resulting in better generalization and performance. PHEW achieves significant improvements over the data-independent SynFlow and SynFlow-L2 methods at a wide range of network densities.
翻译:在初始化时扩大网络的方法在实践中很重要,因为它们大大提高了学习和推导的效率。我们的工作基于最近提出的将培训过程的动态分解成一个数据依赖部分和结构依赖的内核的方法,后者被称为路径中内核。这项工作表明如何在没有任何培训数据的情况下,利用Synflow-L2算法,设计稀疏神经网络,以便更快地汇合。我们首先表明,即使同步流-L2在趋同方面是最佳的,对于特定的网络密度而言,它也是最佳的,但是,它的结果是,与使用相同数量的参数的其他数据-认知方法相比,它分解了培训过程的动态。然后,我们提出了一个在没有任何培训数据的情况下,建立稀少网络的新方法,称为高视野路径(PHEW)。PHEW是一种建立在偏差随机随机行走上的网络形成稳定性化方法,仅取决于初始的网络密度密度,它的结果是“瓶颈”(窄)层的子网络,结果与使用同样数量的运行方式在同步水平上产生类似的路径性改进。