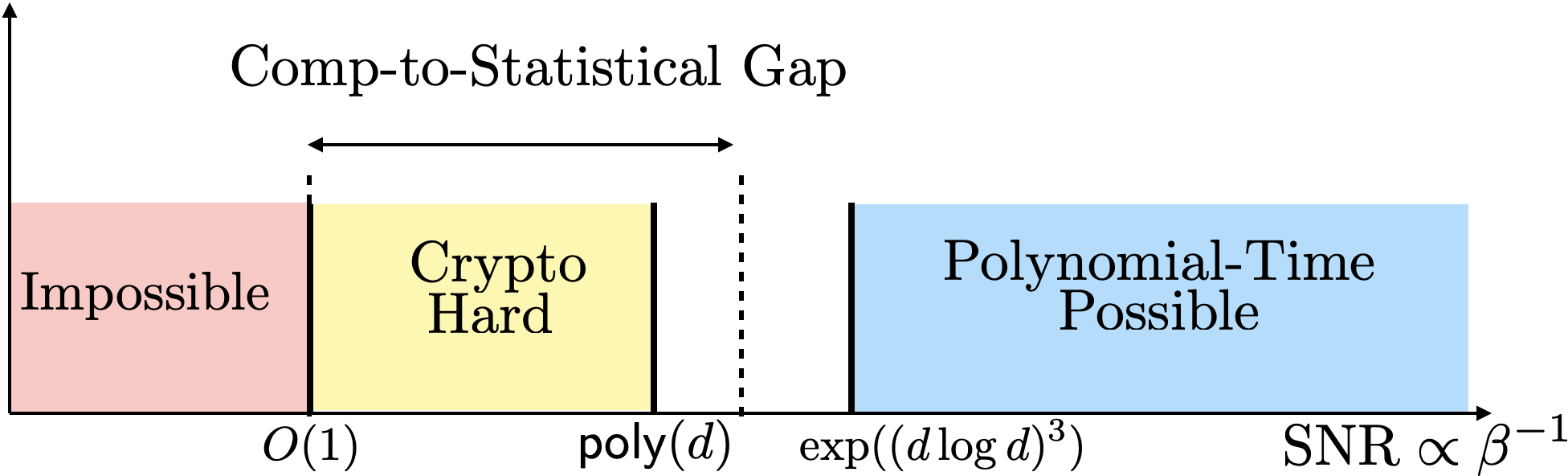
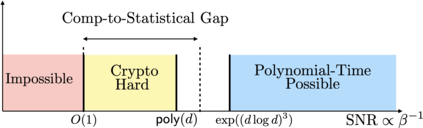
We show a simple reduction which demonstrates the cryptographic hardness of learning a single periodic neuron over isotropic Gaussian distributions in the presence of noise. More precisely, our reduction shows that any polynomial-time algorithm (not necessarily gradient-based) for learning such functions under small noise implies a polynomial-time quantum algorithm for solving worst-case lattice problems, whose hardness form the foundation of lattice-based cryptography. Our core hard family of functions, which are well-approximated by one-layer neural networks, take the general form of a univariate periodic function applied to an affine projection of the data. These functions have appeared in previous seminal works which demonstrate their hardness against gradient-based (Shamir'18), and Statistical Query (SQ) algorithms (Song et al.'17). We show that if (polynomially) small noise is added to the labels, the intractability of learning these functions applies to all polynomial-time algorithms, beyond gradient-based and SQ algorithms, under the aforementioned cryptographic assumptions. Moreover, we demonstrate the necessity of noise in the hardness result by designing a polynomial-time algorithm for learning certain families of such functions under exponentially small adversarial noise. Our proposed algorithm is not a gradient-based or an SQ algorithm, but is rather based on the celebrated Lenstra-Lenstra-Lov\'asz (LLL) lattice basis reduction algorithm. Furthermore, in the absence of noise, this algorithm can be directly applied to solve CLWE detection (Bruna et al.'21) and phase retrieval with an optimal sample complexity of $d+1$ samples. In the former case, this improves upon the quadratic-in-$d$ sample complexity required in (Bruna et al.'21).
翻译:我们展示了一个简单的减法, 这表明了学习单一周期性神经神经的加密难度。 更准确地说, 我们的减法显示, 在小噪音下学习这些功能的任何多元时算算法( 不一定以梯度为基础) 意味着一个解决最坏情况拉特的多式量算法, 其硬性构成基于加密的基础。 我们的核心硬性函数组合, 由一层的神经网络所接近的复杂度, 采取一个普通的单量定期函数的形式, 用于对数据进行直线投。 更准确地说, 我们的减法显示, 这些函数出现在以前的半量算法中, 显示它们对于基于梯度的( Shamir' 18) 和SQ( SQ ) 的硬性定量算法, 表明如果( 极性) 小量级的噪音被添加到提议的标签中, 学习这些函数的易性能性能适用于所有多时算法, 超越基于梯度和SQ值的直值定期计算法, 。 在前级的变法中, 以某种硬性变数级的变数性算法, 。