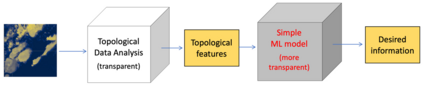
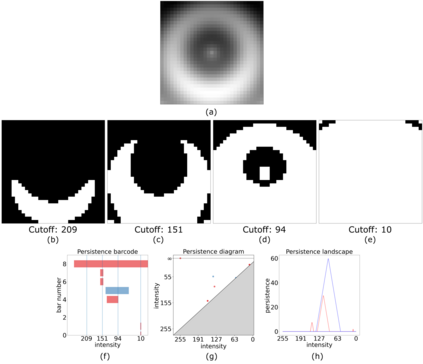
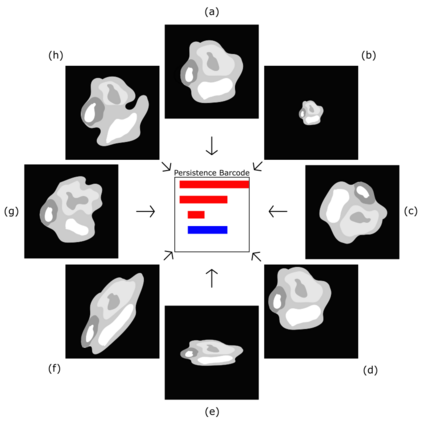
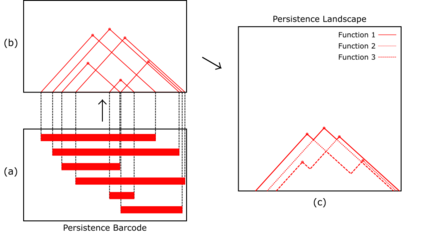
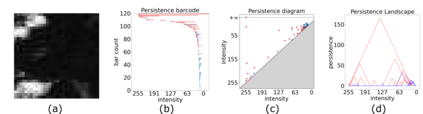
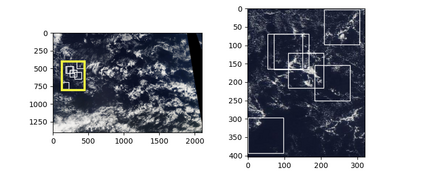
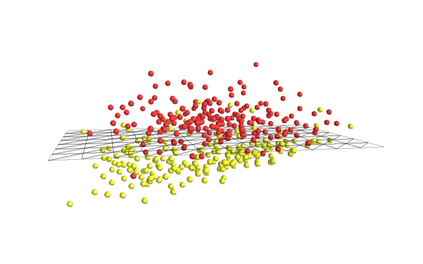
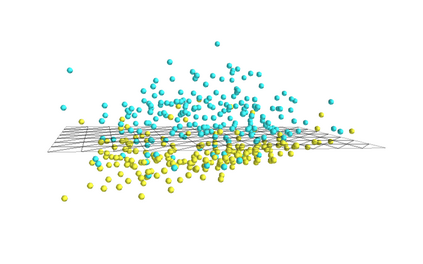
Topological data analysis (TDA) is a tool from data science and mathematics that is beginning to make waves in environmental science. In this work, we seek to provide an intuitive and understandable introduction to a tool from TDA that is particularly useful for the analysis of imagery, namely persistent homology. We briefly discuss the theoretical background but focus primarily on understanding the output of this tool and discussing what information it can glean. To this end, we frame our discussion around a guiding example of classifying satellite images from the Sugar, Fish, Flower, and Gravel Dataset produced for the study of mesocale organization of clouds by Rasp et. al. in 2020 (arXiv:1906:01906). We demonstrate how persistent homology and its vectorization, persistence landscapes, can be used in a workflow with a simple machine learning algorithm to obtain good results, and explore in detail how we can explain this behavior in terms of image-level features. One of the core strengths of persistent homology is how interpretable it can be, so throughout this paper we discuss not just the patterns we find, but why those results are to be expected given what we know about the theory of persistent homology. Our goal is that a reader of this paper will leave with a better understanding of TDA and persistent homology, be able to identify problems and datasets of their own for which persistent homology could be helpful, and gain an understanding of results they obtain from applying the included GitHub example code.
翻译:地形数据分析(TDA)是一个来自数据科学和数学的工具,它开始在环境科学中制造波浪。在这项工作中,我们力求为来自TDA的工具提供一个直观和可理解的导言,该工具对图像分析特别有用,即持久性同质学。我们简要讨论理论背景,但主要侧重于了解这一工具的输出,并讨论它能够收集哪些信息。为此,我们的讨论围绕一个指导性范例进行,即对来自糖、鱼、花卉和Gravel数据集的卫星图像进行分类,这些图像是Rasp等人为2020年为研究2020年云层的中观组织而制作的(arXiv:1906:01906:906)。 我们展示了如何在一个工作流程中使用持久性同质学及其矢量化、持久性地貌景观来使用,以获得良好的效果,并详细探讨我们如何用图像层面的特点来解释这种行为。持续同理学的核心优点之一,是可以解释的,因此在整个文件中我们不仅讨论我们所找到的模式,而且我们为什么这些结果能够被期待到一个我们所了解的、我们所了解的、我们所了解的、我们所了解的同系的、我们所了解的、我们所了解的同理学的、我们所了解的、我们所了解的、我们所持的、我们所持的理论的理论的理论的理论的理论将有一个的理论的理论将更能确定一个更清楚。