Isotonic subgroup selection

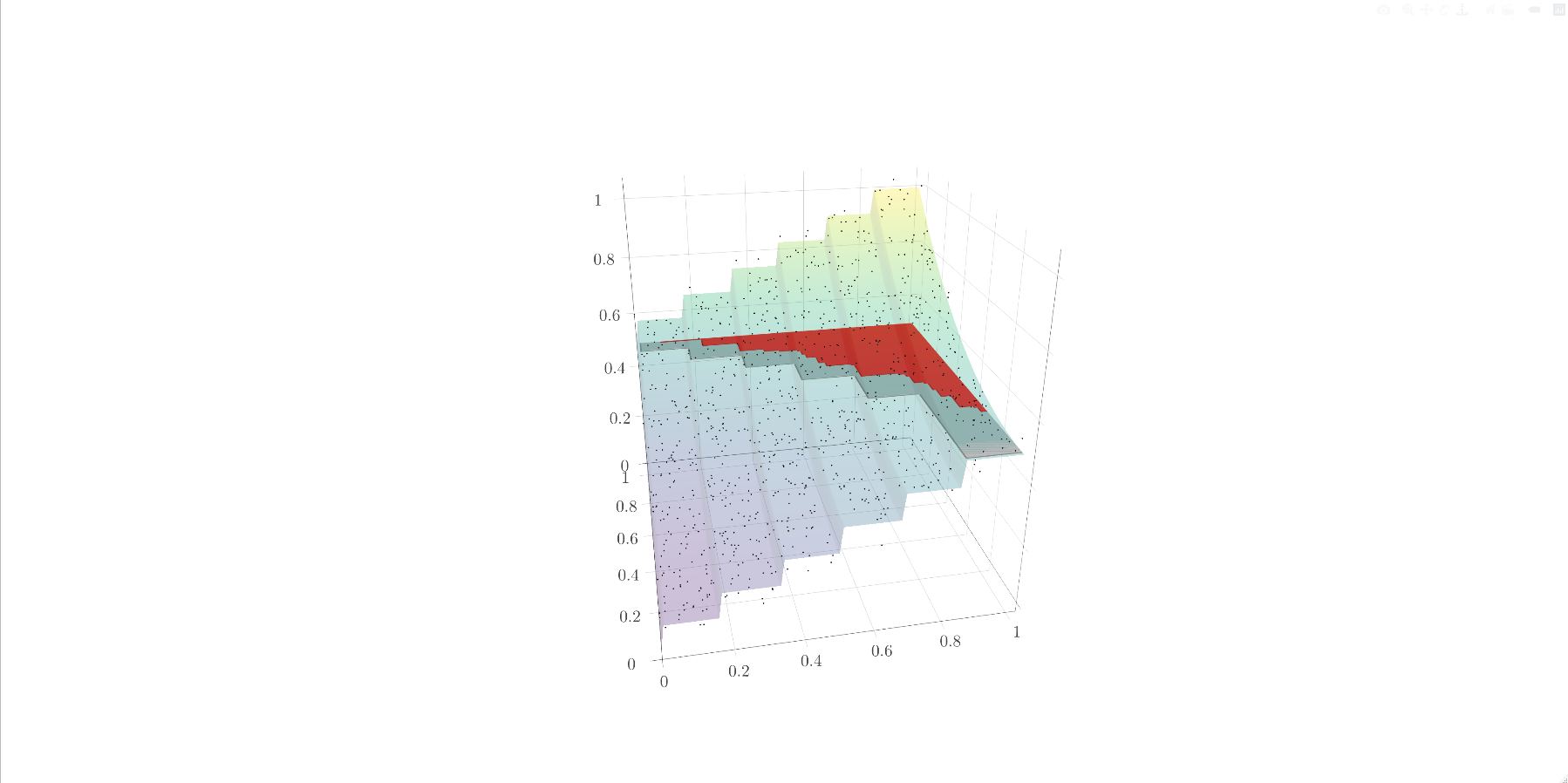
Given a sample of covariate-response pairs, we consider the subgroup selection problem of identifying a subset of the covariate domain where the regression function exceeds a pre-determined threshold. We introduce a computationally-feasible approach for subgroup selection in the context of multivariate isotonic regression based on martingale tests and multiple testing procedures for logically-structured hypotheses. Our proposed procedure satisfies a non-asymptotic, uniform Type I error rate guarantee with power that attains the minimax optimal rate up to poly-logarithmic factors. Extensions cover classification, isotonic quantile regression and heterogeneous treatment effect settings. Numerical studies on both simulated and real data confirm the practical effectiveness of our proposal.