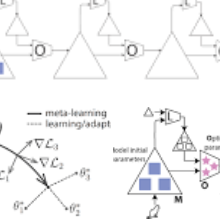
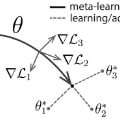
Meta-learning aims to solve unseen tasks with few labelled instances. Nevertheless, despite its effectiveness for quick learning in existing optimization-based methods, it has several flaws. Inconsequential connections are frequently seen during meta-training, which results in an over-parameterized neural network. Because of this, meta-testing observes unnecessary computations and extra memory overhead. To overcome such flaws. We propose a novel meta-learning method called Meta-LTH that includes indispensible (necessary) connections. We applied the lottery ticket hypothesis technique known as magnitude pruning to generate these crucial connections that can effectively solve few-shot learning problem. We aim to perform two things: (a) to find a sub-network capable of more adaptive meta-learning and (b) to learn new low-level features of unseen tasks and recombine those features with the already learned features during the meta-test phase. Experimental results show that our proposed Met-LTH method outperformed existing first-order MAML algorithm for three different classification datasets. Our method improves the classification accuracy by approximately 2% (20-way 1-shot task setting) for omniglot dataset.
翻译:元学习旨在使用少量标记实例解决未知的任务。然而,尽管它在现有的基于优化的方法中对快速学习非常有效,但它仍存在一些缺陷。在元训练过程中经常出现不必要的连接,导致过度参数化的神经网络。由于这个原因,元测试观察到不必要的计算和额外的内存开销。为了克服这些缺点,我们提出了一种新的元学习方法,称为 Meta-LTH,包括必要的连接。我们应用了被称为大小剪枝的幸存彩票假说技术来生成这些关键连接,可以有效地解决少样本学习问题。我们的目标是实现两个方面:(a) 找到更适应元学习的子网络,和 (b) 在元测试阶段学习未知任务的新低级特征,并将这些特征与已经学习过的特征重新组合。实验结果表明,我们提出的 Meta-LTH 方法在三个不同的分类数据集上优于现有的一阶 MAML 算法。我们的方法提高了 Omniglot 数据集在 20 分类 1 拍摄任务设置下的分类准确率约 2%。