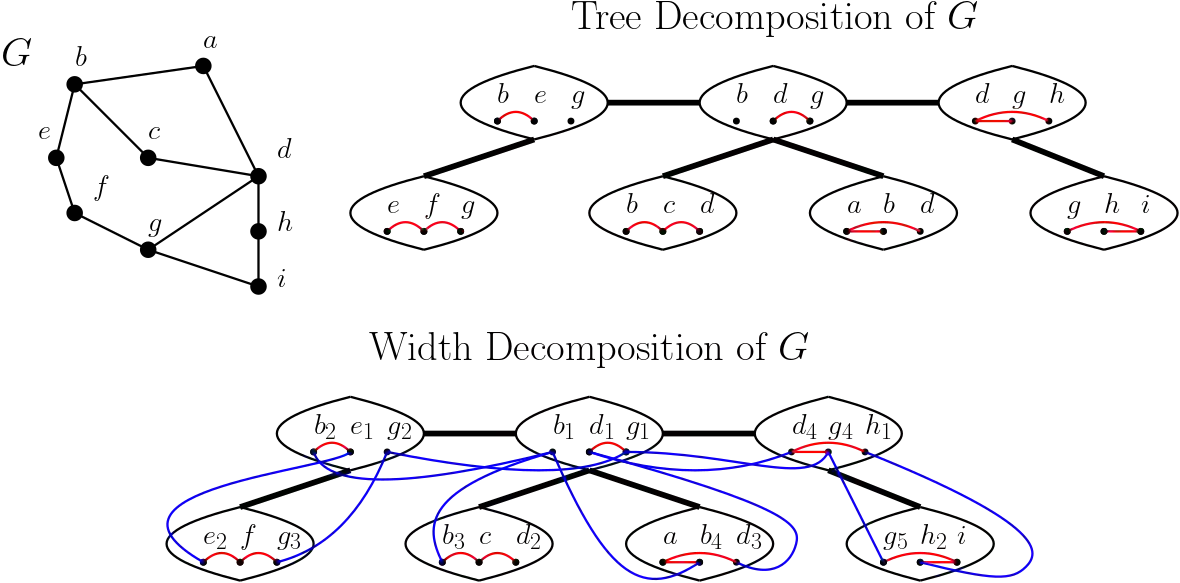
We prove an approximate max-multiflow min-multicut theorem for bounded treewidth graphs. In particular, we show the following: Given a treewidth-$r$ graph, there exists a (fractional) multicommodity flow of value $f$, and a multicut of capacity $c$ such that $ f \leq c \leq \mathcal{O}(\ln (r+1)) \cdot f$. It is well known that the multiflow-multicut gap on an $r$-vertex (constant degree) expander graph can be $\Omega(\ln r)$, and hence our result is tight up to constant factors. Our proof is constructive, and we also obtain a polynomial time $\mathcal{O}(\ln (r+1))$-approximation algorithm for the minimum multicut problem on treewidth-$r$ graphs. Our algorithm proceeds by rounding the optimal fractional solution to the natural linear programming relaxation of the multicut problem. We introduce novel modifications to the well-known region growing algorithm to facilitate the rounding while guaranteeing at most a logarithmic factor loss in the treewidth.
翻译:我们证明,对于捆绑的树枝图形,我们是一个近乎最大-多流的多倍点理论。特别是,我们展示了以下内容:在树形-美元图中,存在一个价值f美元(f$)的(折合)多通货流,一个能力方块的(折合的)美元倍数,例如,美元=leq c\leq\leq\mathcal{O}(ln)\(r+1))\cdot f$。众所周知,一个美元-垂直(常态)扩展图上的多流-多流差可以是$(Omega-ln r),因此我们的结果接近于恒定因素。我们的证据是建设性的,我们还获得了一个用于树形-$(r+1)最小多立点问题的多元度算法。我们的算法通过将最佳的分数解决方案四舍四舍五入到自然线性编程变换速度,从而在最清楚的树形区域引入了新式的传算法,同时,我们引入了最清楚的缩算法,以保证了圆形的损区域。