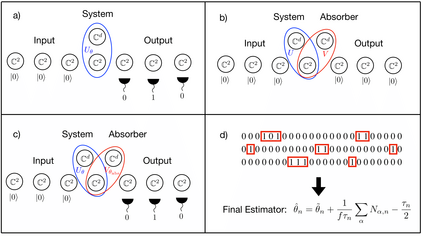
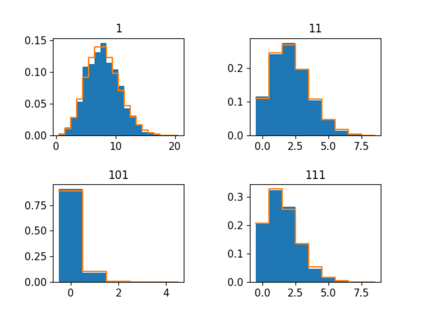
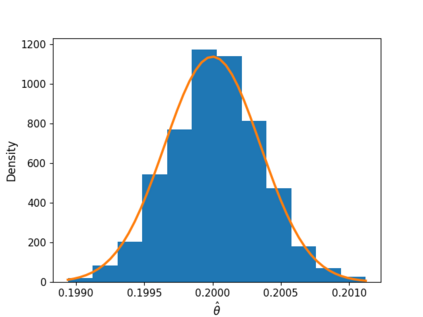
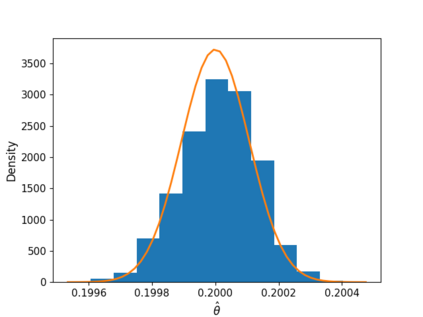
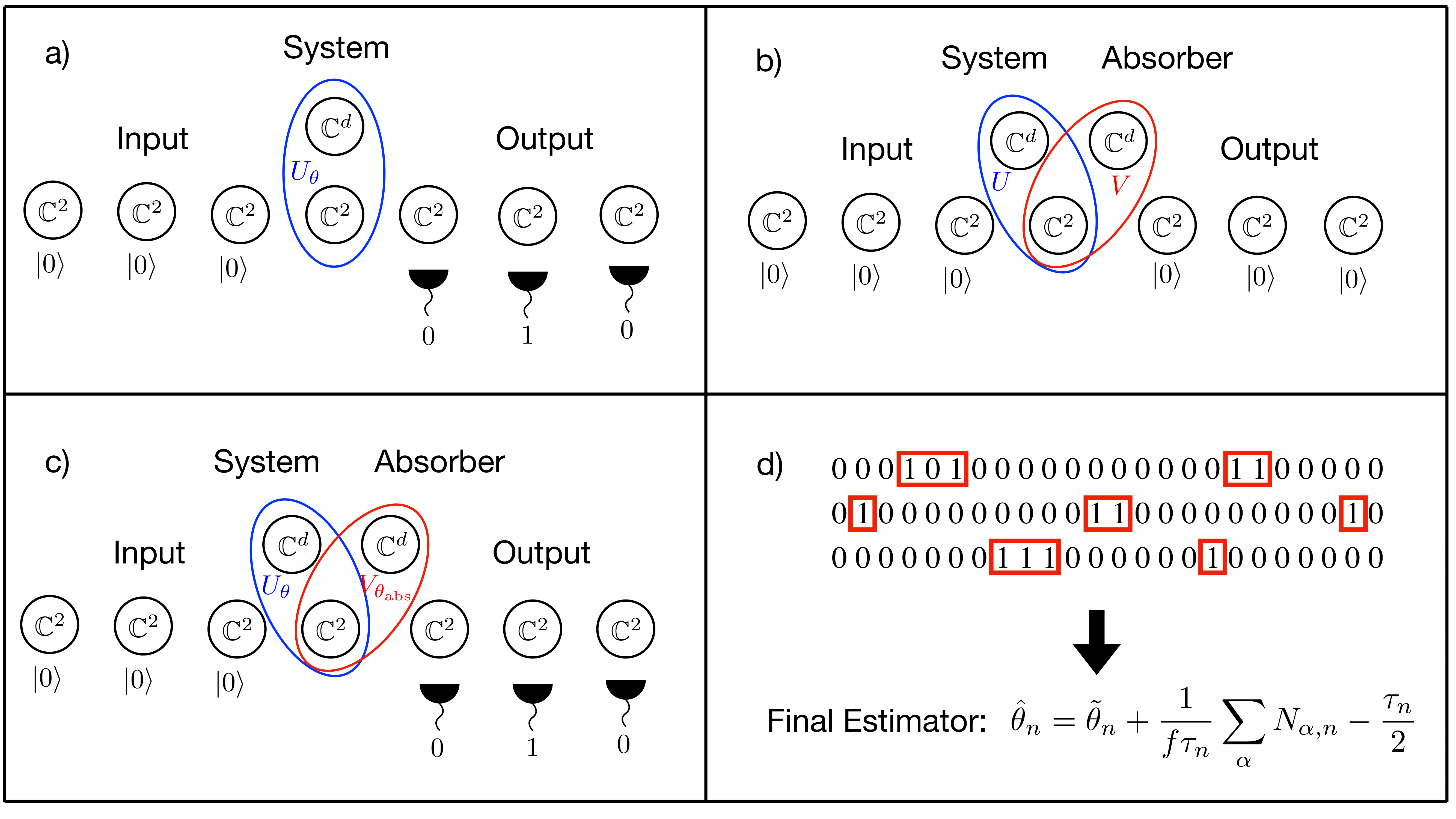
We propose a two step strategy for estimating one-dimensional dynamical parameters of a quantum Markov chain, which involves quantum post-processing the output using a coherent quantum absorber and a "pattern counting'' estimator computed as a simple additive functional of the outcomes trajectory produced by sequential, identical measurements on the output units. We provide strong theoretical and numerical evidence that the estimator achieves the quantum Cram\'{e}-Rao bound in the limit of large output size. Our estimation method is underpinned by an asymptotic theory of translationally invariant modes (TIMs) built as averages of shifted tensor products of output operators, labelled by binary patterns. For large times, the TIMs form a bosonic algebra and the output state approaches a joint coherent state of the TIMs whose amplitude depends linearly on the mismatch between system and absorber parameters. Moreover, in the asymptotic regime the TIMs capture the full quantum Fisher information of the output state. While directly probing the TIMs' quadratures seems impractical, we show that the standard sequential measurement is an effective joint measurement of all the TIMs number operators; indeed, we show that counts of different binary patterns extracted from the measurement trajectory have the expected joint Poisson distribution. Together with the displaced-null methodology of J. Phys. A: Math. Theor. 57 245304 2024 this provides a computationally efficient estimator which only depends on the total number of patterns. This opens the way for similar estimation strategies in continuous-time dynamics, expanding the results of Phys. Rev. X 13, 031012 2023.
翻译:暂无翻译