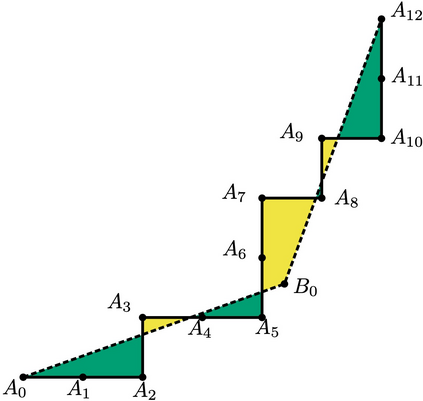
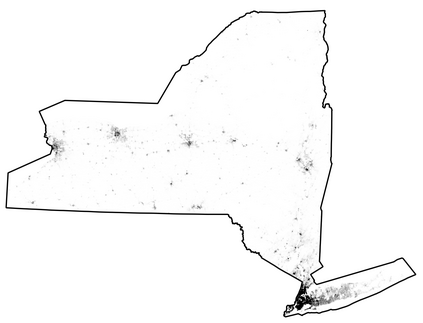
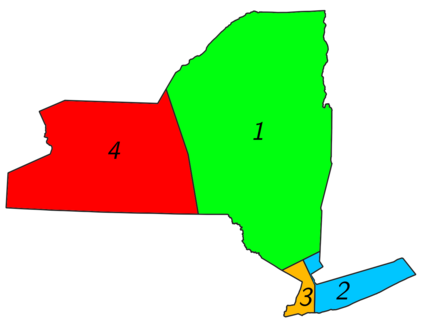
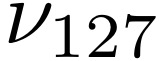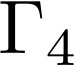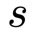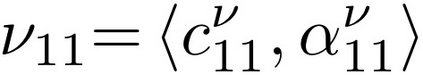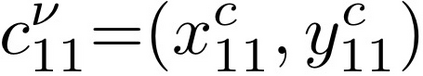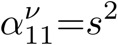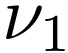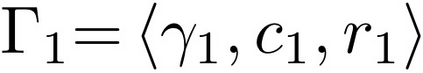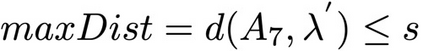In this paper, we consider the problem of partitioning a polygon into a set of connected disjoint sub-polygons, each of which covers an area of a specific size. The work is motivated by terrain covering applications in robotics, where the goal is to find a set of efficient plans for a team of heterogeneous robots to cover a given area. Within this application, solving a polygon partitioning problem is an essential stepping stone. Unlike previous work, the problem formulation proposed in this paper also considers a compactness metric of the generated sub-polygons, in addition to the area size constraints. Maximizing the compactness of sub-polygons directly influences the optimality of any generated motion plans. Consequently, this increases the efficiency with which robotic tasks can be performed within each sub-region. The proposed problem representation is based on grid cell decomposition and a potential field model that allows for the use of standard optimization techniques. A new algorithm, the AreaDecompose algorithm, is proposed to solve this problem. The algorithm includes a number of existing and new optimization techniques combined with two post-processing methods. The approach has been evaluated on a set of randomly generated polygons which are then divided using different criteria and the results have been compared with a state-of-the-art algorithm. Results show that the proposed algorithm can efficiently divide polygon regions maximizing compactness of the resulting partitions, where the sub-polygon regions are on average up to 73% more compact in comparison to existing techniques.
翻译:在本文中, 我们考虑将一个多边形分割成一组相联的分解分解分形形形体的问题, 每一组都覆盖一个特定大小的面积。 这项工作的动机是机器人应用的地形, 目的是为一组多元机器人寻找一套有效的计划, 以覆盖一个特定区域。 在此应用中, 解决多边形分区问题是一个必要的垫脚石。 与先前的工作不同, 本文中建议的问题提法还考虑对生成的子形形形体的缩缩略度度, 除了区域大小的限制之外, 也考虑对生成的子形形形形形形形形形形形形形形形形形形形形形形形形形形形形色形形形形形形形形形色的缩缩缩缩缩缩缩缩缩, 直接影响到任何生成的动作图色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色的缩图。, 和相形色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色区域,,, 、 、 等色色色色色色色色色色色色色色色色色色色色区域, 等色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色图,,,, 等, 等等等等等等等等等等等等等等等