Optimistic Policy Iteration for MDPs with Acyclic Transient State Structure

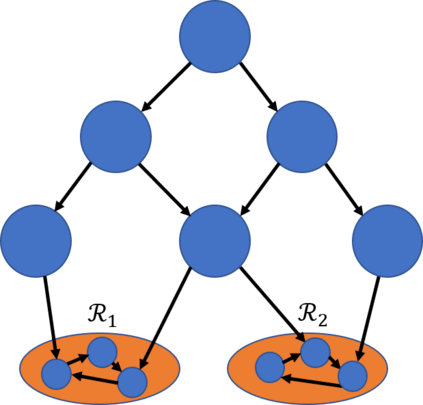
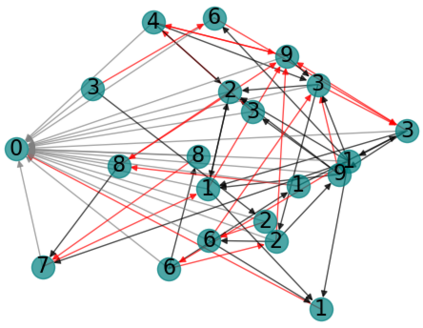
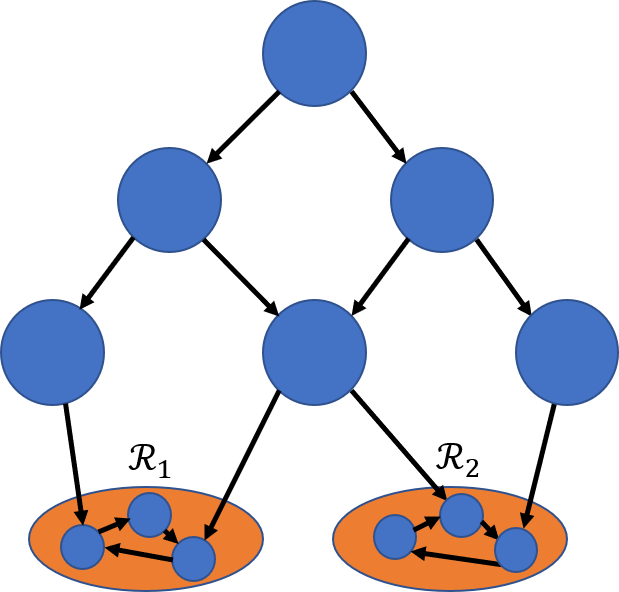
We consider Markov Decision Processes (MDPs) in which every stationary policy induces the same graph structure for the underlying Markov chain and further, the graph has the following property: if we replace each recurrent class by a node, then the resulting graph is acyclic. For such MDPs, we prove the convergence of the stochastic dynamics associated with a version of optimistic policy iteration (OPI), suggested in Tsitsiklis (2002), in which the values associated with all the nodes visited during each iteration of the OPI are updated.