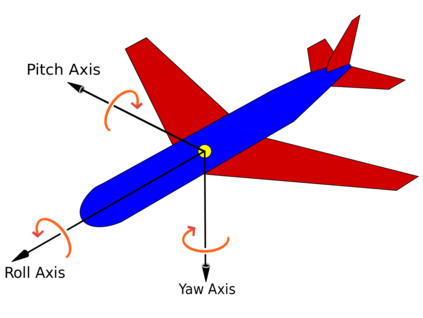
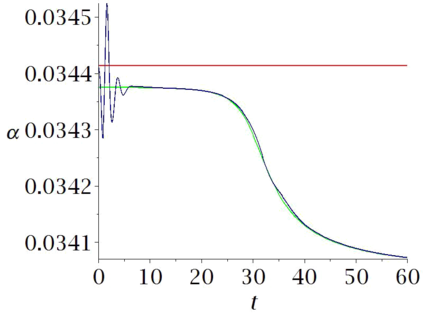
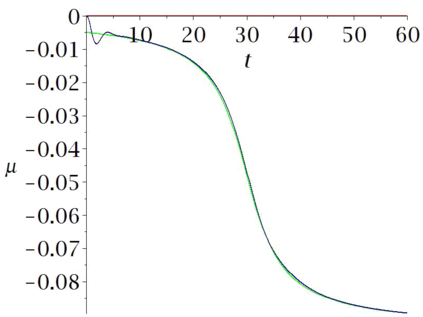
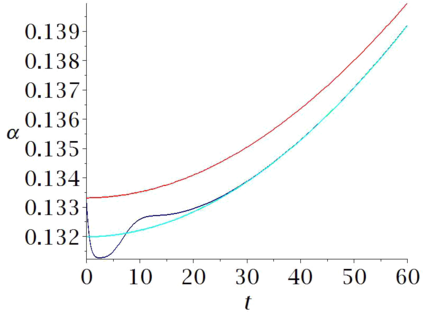
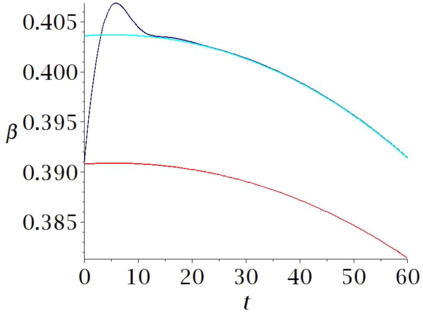
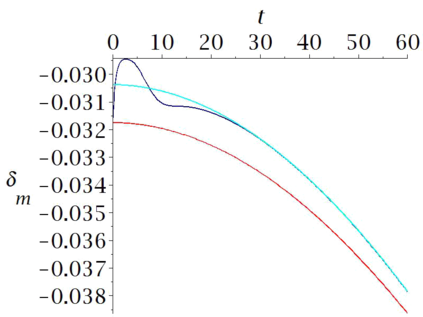
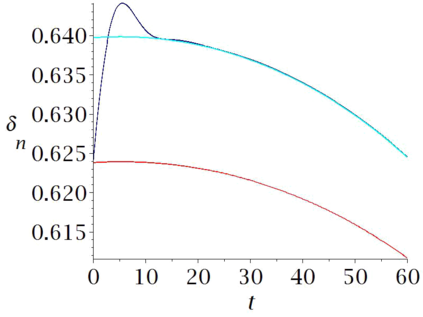
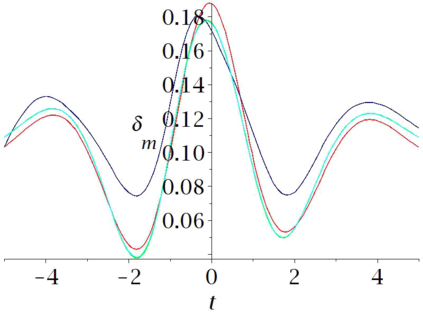
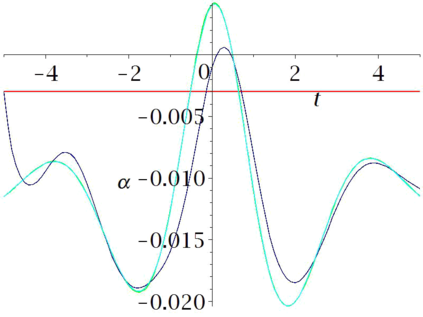
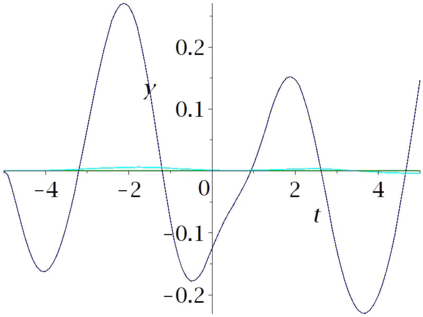
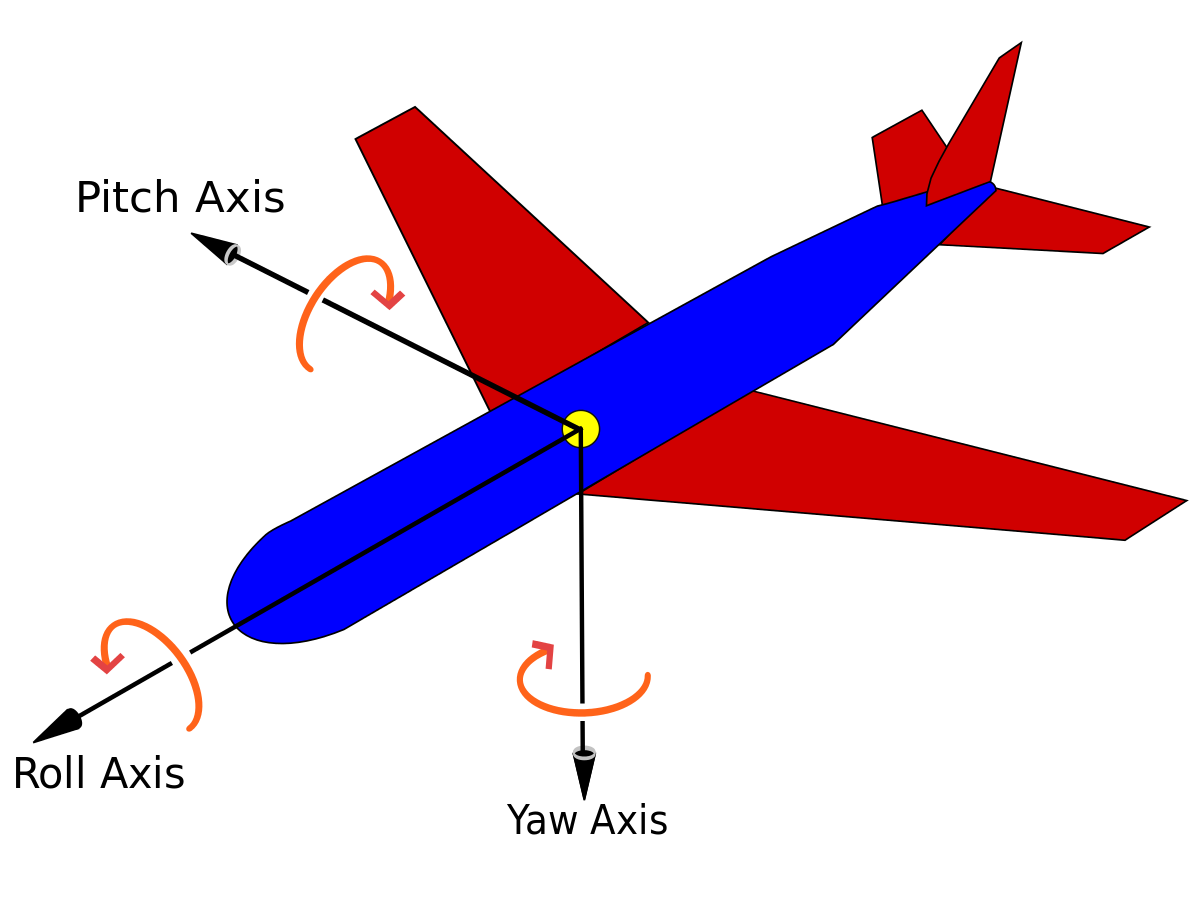
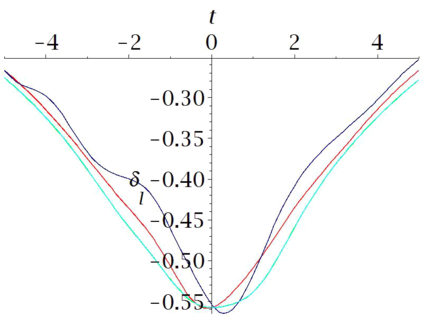Aircraft models may be considered as flat if one neglects some terms associated to aerodynamics. Computational experiments in Maple show that in some cases a suitably designed feed-back allows to follow such trajectories, when applied to the non-flat model. However some maneuvers may be hard or even impossible to achieve with this flat approximation. In this paper, we propose an iterated process to compute a more achievable trajectory, starting from the flat reference trajectory. More precisely, the unknown neglected terms in the flat model are iteratively re-evaluated using the values obtained at the previous step. This process may be interpreted as a new trajectory parametrization, using an infinite number of derivatives, a property that may be called \emph{generalized flatness}. We illustrate the pertinence of this approach in flight conditions of increasing difficulties, from single engine flight, to aileron roll.
翻译:如果忽略了与空气动力学有关的某些术语,则航空器模型可能被视为平坦的。在Mamele的计算实验表明,在某些情况下,适当设计的回馈回馈在应用到非加速模型时允许跟踪这种轨迹。然而,使用这种平准近似可能很难或甚至不可能实现某些动作。在本文中,我们建议从平坦的参照轨道开始,用一个迭代的过程来计算一个更可实现的轨道。更确切地说,使用前一步获得的数值,对平准模型中未知的被忽视的术语进行迭代再评价。这一过程可以被解释为一种新的轨迹对称平衡法,使用无限数量的衍生物,这种财产可能被称为“emph{一般平坦度”。我们用从单引擎飞行到弧滚的日益困难的飞行条件来说明这一方法的适切性。