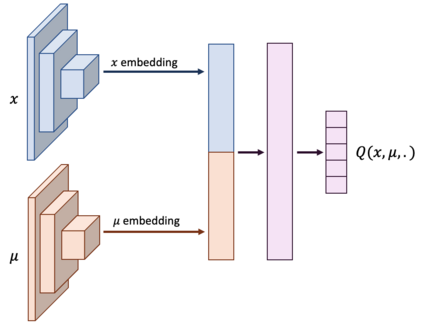
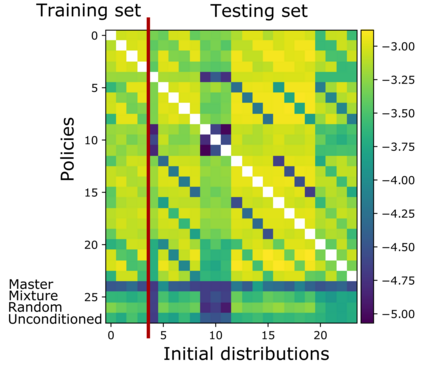
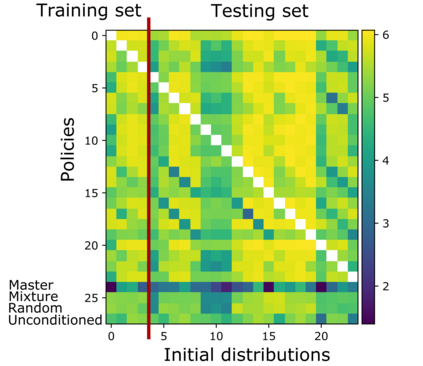
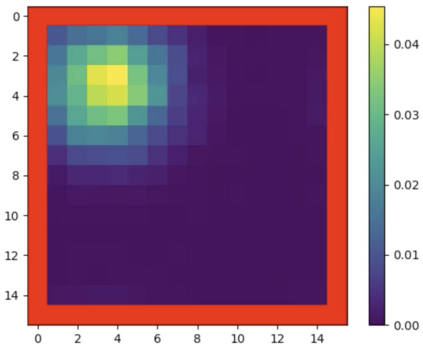
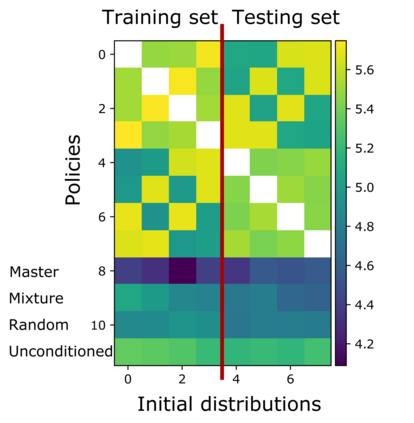
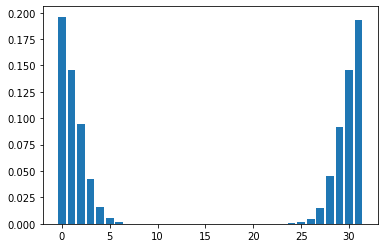
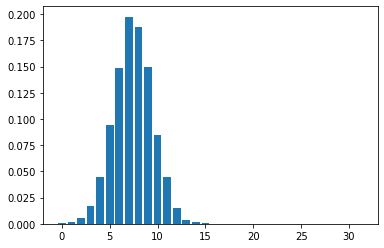
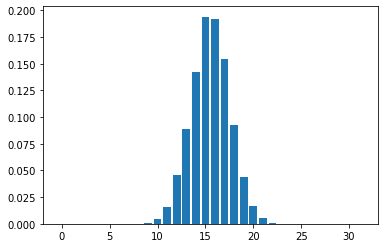
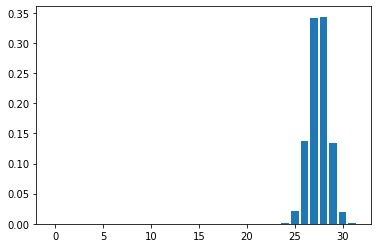
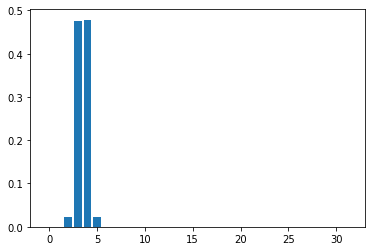
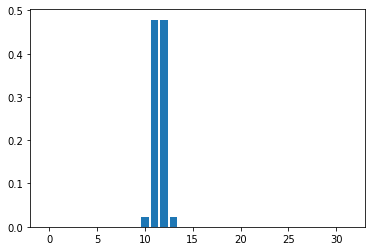
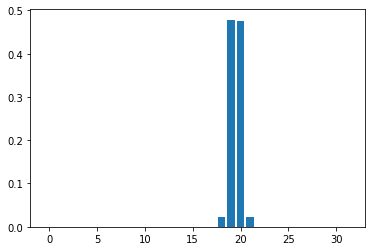
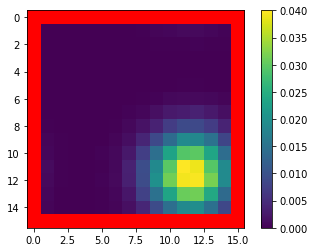
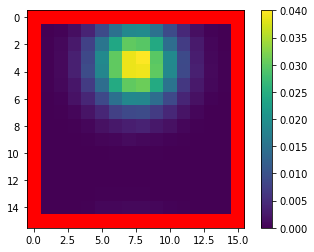
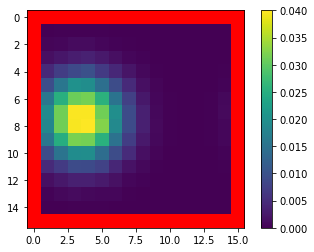
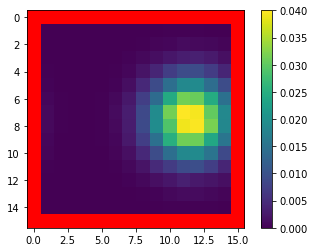
Mean Field Games (MFGs) can potentially scale multi-agent systems to extremely large populations of agents. Yet, most of the literature assumes a single initial distribution for the agents, which limits the practical applications of MFGs. Machine Learning has the potential to solve a wider diversity of MFG problems thanks to generalizations capacities. We study how to leverage these generalization properties to learn policies enabling a typical agent to behave optimally against any population distribution. In reference to the Master equation in MFGs, we coin the term ``Master policies'' to describe them and we prove that a single Master policy provides a Nash equilibrium, whatever the initial distribution. We propose a method to learn such Master policies. Our approach relies on three ingredients: adding the current population distribution as part of the observation, approximating Master policies with neural networks, and training via Reinforcement Learning and Fictitious Play. We illustrate on numerical examples not only the efficiency of the learned Master policy but also its generalization capabilities beyond the distributions used for training.
翻译:平面运动会(MFGs)有可能将多试剂系统扩大至极其庞大的代理群体。然而,大多数文献假设对代理机构进行单一的初步分配,从而限制MFGs的实际应用。机器学习由于一般化能力,有可能解决更广泛的MFG问题。我们研究如何利用这些一般化特性来学习政策,使典型的代理机构能够针对任何人口分布采取最佳行为。关于MFGs的总等式,我们用“Master政策”一词来描述它们,我们证明单一的总政策提供了纳什平衡,不管最初的分配如何。我们建议了一种学习这种主政策的方法。我们的方法依靠三个要素:将目前的人口分布作为观察的一部分,与神经网络相近,以及通过加强学习和玩耍进行培训。我们不仅用数字例子来说明所学的总政策的效率,而且用除用于培训的分配之外,还用其一般化能力来说明数字例子。