A Theory of General Difference in Continuous and Discrete Domain

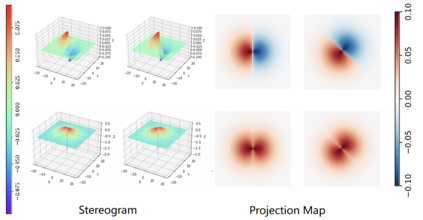
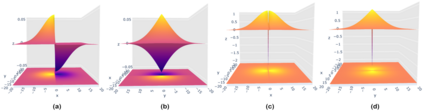
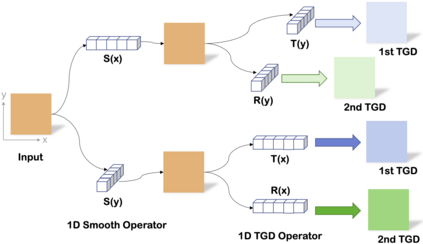
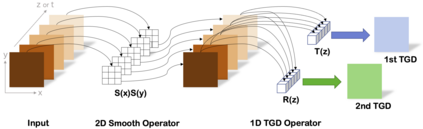
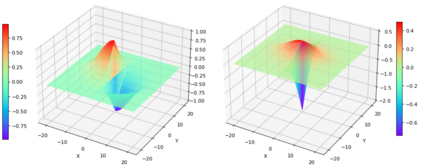
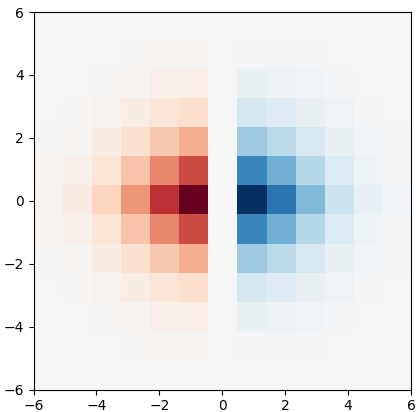
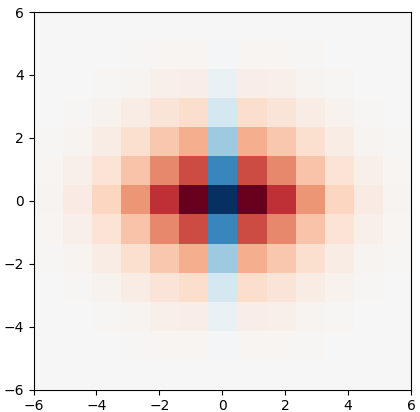
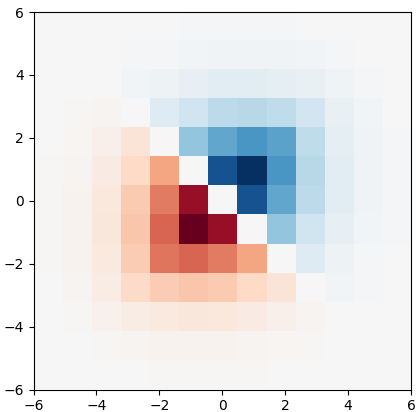
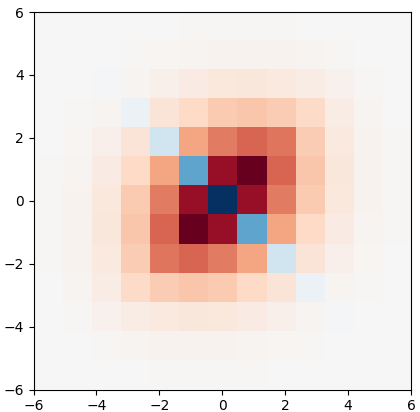
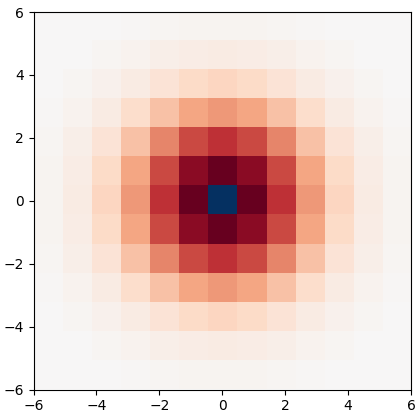
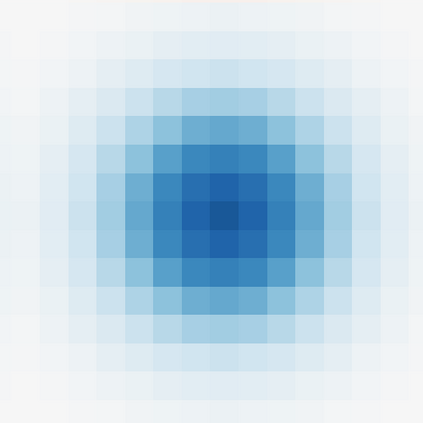
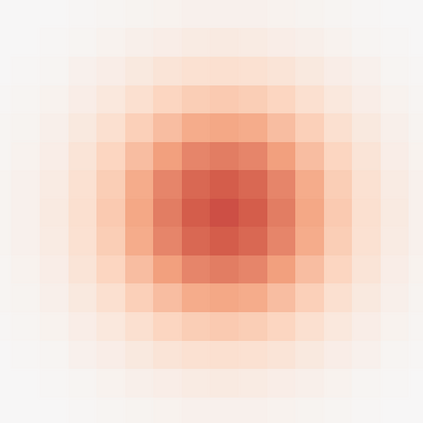
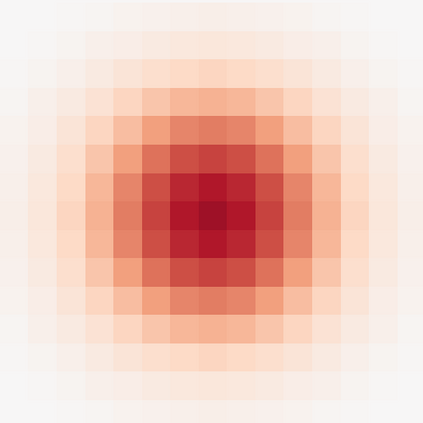
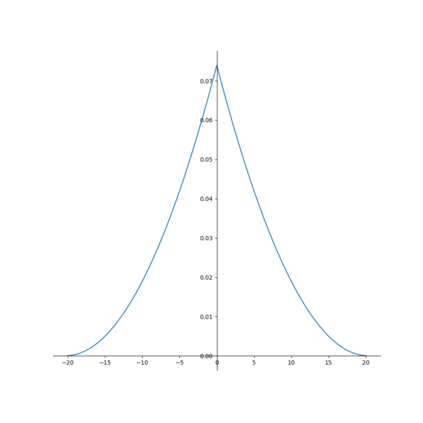
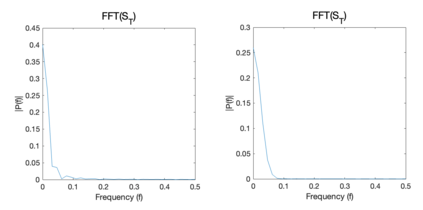
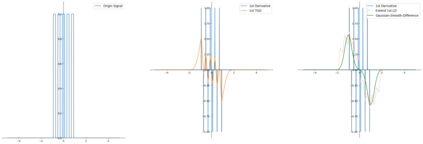
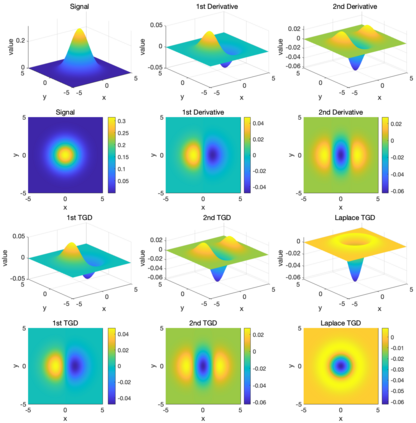
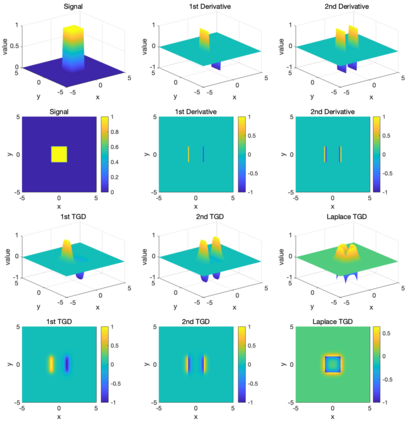
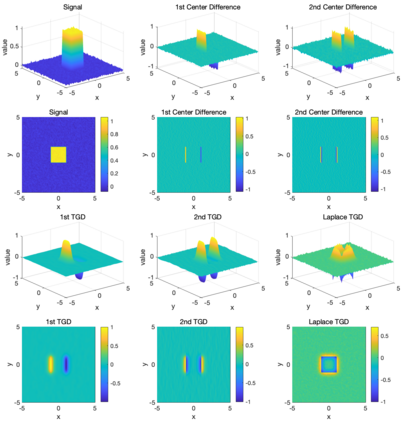
Though a core element of the digital age, numerical difference algorithms struggle with noise susceptibility. This stems from a key disconnect between the infinitesimal quantities in continuous differentiation and the finite intervals in its discrete counterpart. This disconnect violates the fundamental definition of differentiation (Leibniz and Cauchy). To bridge this gap, we build a novel general difference (Tao General Difference, TGD). Departing from derivative-by-integration, TGD generalizes differentiation to finite intervals in continuous domains through three key constraints. This allows us to calculate the general difference of a sequence in discrete domain via the continuous step function constructed from the sequence. Two construction methods, the rotational construction and the orthogonal construction, are proposed to construct the operators of TGD. The construction TGD operators take same convolution mode in calculation for continuous functions, discrete sequences, and arrays across any dimension. Our analysis with example operations showcases TGD's capability in both continuous and discrete domains, paving the way for accurate and noise-resistant differentiation in the digital era.