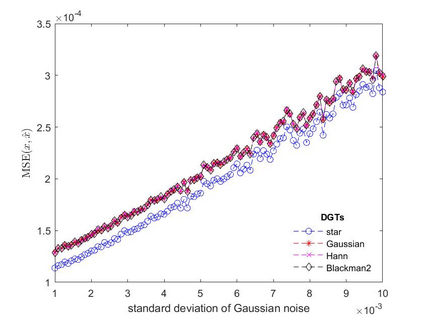
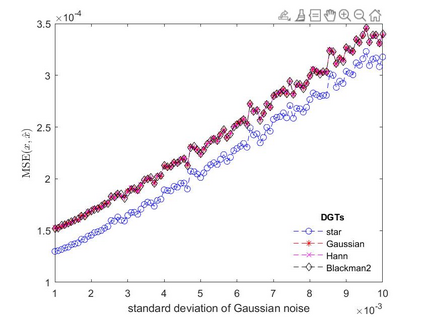
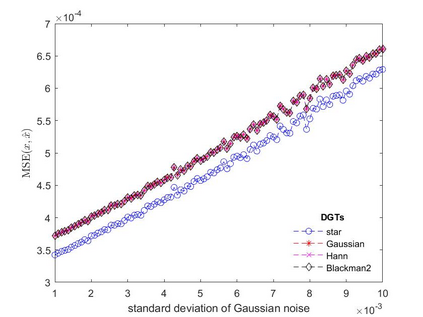
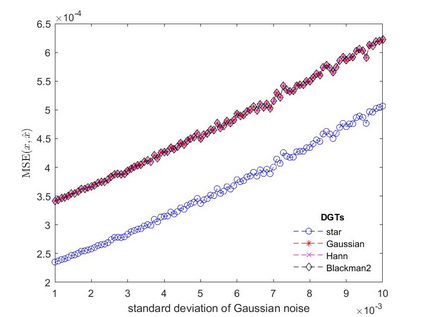
In this paper, we address the speech denoising problem, where white Gaussian additive noise is to be removed from a given speech signal. Our approach is based on a redundant, analysis-sparse representation of the original speech signal. We pick an eigenvector of the Zauner unitary matrix and -- under certain assumptions on the ambient dimension -- we use it as window vector to generate a spark deficient Gabor frame. The analysis operator associated with such a frame, is a (highly) redundant Gabor transform, which we use as a sparsifying transform in denoising procedure. We conduct computational experiments on real-world speech data, solving the analysis basis pursuit denoising problem, with four different choices of analysis operators, including our Gabor analysis operator. The results show that our proposed redundant Gabor transform outperforms -- in all cases -- Gabor transforms generated by state-of-the-art window vectors of time-frequency analysis.
翻译:在本文中,我们解决了语言分解问题, 白高斯语添加性噪音将从特定语言信号中去除。 我们的方法是基于对原始语音信号的冗余、 分析偏差的表达方式。 我们选择了Zauner 单体矩阵的导体, 在环境维度的某些假设下, 我们用它作为窗口矢量, 产生一个火花不足的加博框架。 与此框架相关的分析操作员是一个( 高度) 多余的加博变异, 我们用它来对调离过程的变异进行覆盖。 我们用真实世界的语音数据进行计算实验, 解决分析基础的解调问题, 分析操作员有四种不同的选择, 包括我们的加博分析操作员。 结果表明, 我们提议的冗余加博变异了外形 -- 在所有情况下 -- 加博变异都是由时间频率分析的最新窗口矢量生成的加博变异。