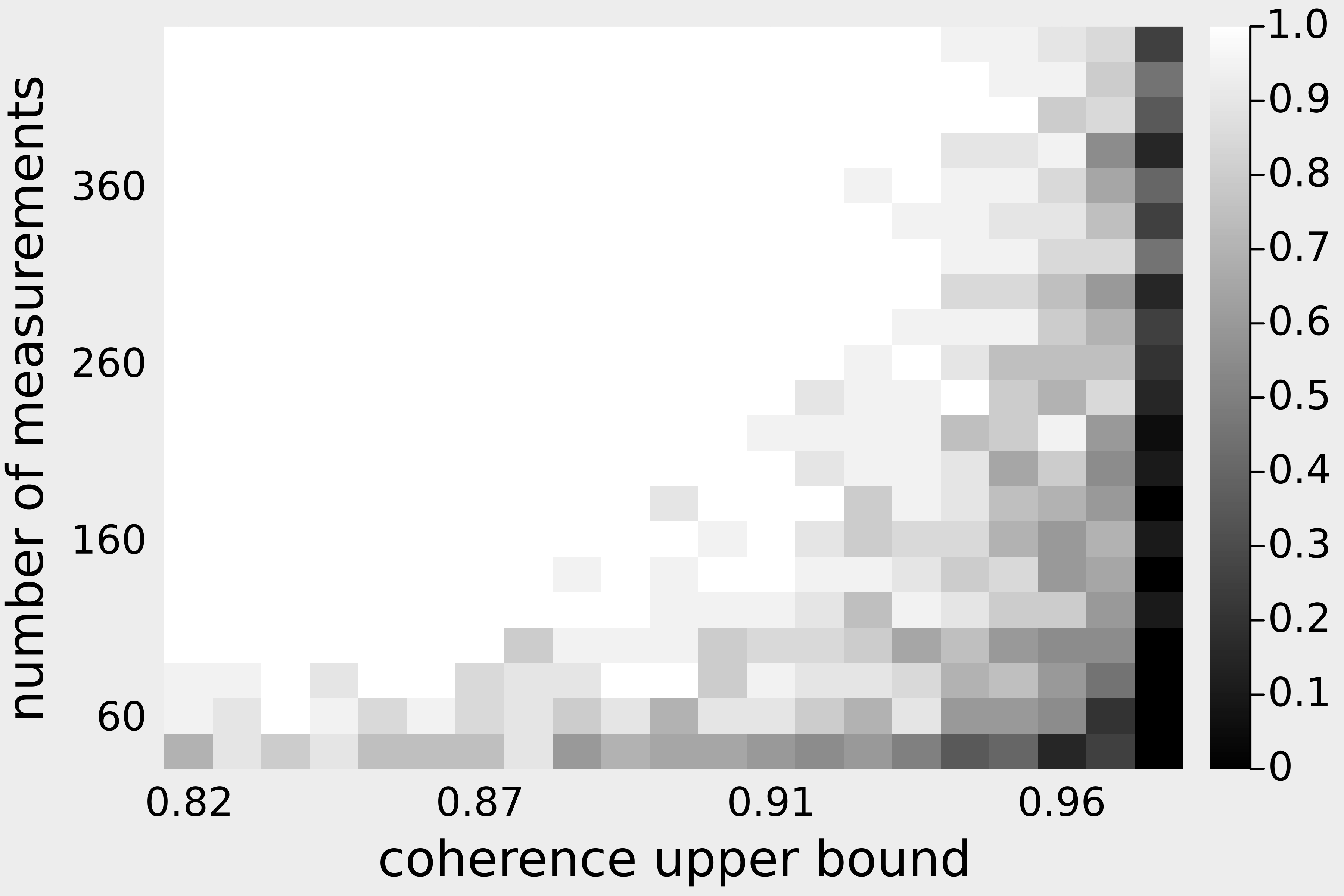
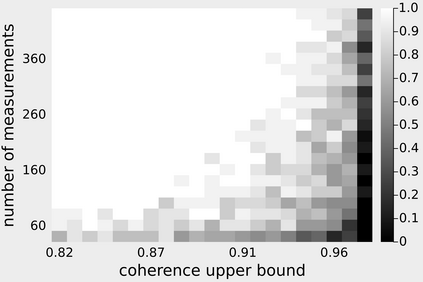
In Bora et al. (2017), a mathematical framework was developed for compressed sensing guarantees in the setting where the measurement matrix is Gaussian and the signal structure is the range of a generative neural network (GNN). The problem of compressed sensing with GNNs has since been extensively analyzed when the measurement matrix and/or network weights follow a subgaussian distribution. We move beyond the subgaussian assumption, to measurement matrices that are derived by sampling uniformly at random rows of a unitary matrix (including subsampled Fourier measurements as a special case). Specifically, we prove the first known restricted isometry guarantee for generative compressed sensing with subsampled isometries and provide recovery bounds, addressing an open problem of Scarlett et al. (2022, p. 10). Recovery efficacy is characterized by the coherence, a new parameter, which measures the interplay between the range of the network and the measurement matrix. Our approach relies on subspace counting arguments and ideas central to high-dimensional probability. Furthermore, we propose a regularization strategy for training GNNs to have favourable coherence with the measurement operator. We provide compelling numerical simulations that support this regularized training strategy: our strategy yields low coherence networks that require fewer measurements for signal recovery. This, together with our theoretical results, supports coherence as a natural quantity for characterizing generative compressed sensing with subsampled isometries.
翻译:在Bora等人(2017年),为测量矩阵为高森,而信号结构为基因神经网络的范围(GNN),在测量矩阵和(或)网络重量的分布发生亚高苏西分布后,对GNN的压缩遥感问题进行了广泛分析。我们超越了亚陆基假设,转向了通过对单一矩阵随机行进行统一抽样得出的测量矩阵(包括作为特例对Fourier测量进行分抽样)。具体地说,我们证明,对以子样样版的异式压缩传感器进行遗传压缩传感器的已知第一种限制性保证,提供了恢复界限,解决了Scarlett等人(2022年,第10页)的公开问题。恢复效果的特点是一致性,这是一个新参数,衡量网络与测量矩阵之间的相互作用。我们的方法依赖于以高度概率为核心的次空间计参数和想法。此外,我们提议了一项正规化战略,用于培训GNNNP与测量操作者保持有利的一致性。我们提供了令人信服的数字模型模拟,用以进行定期的血压测量。