Beyond Gaussian Assumptions: A Nonlinear Generalization of Linear Inverse Modeling

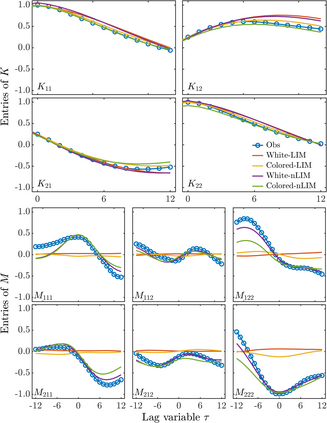
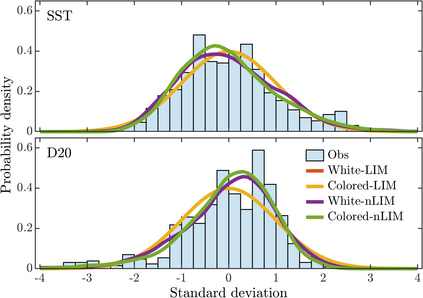
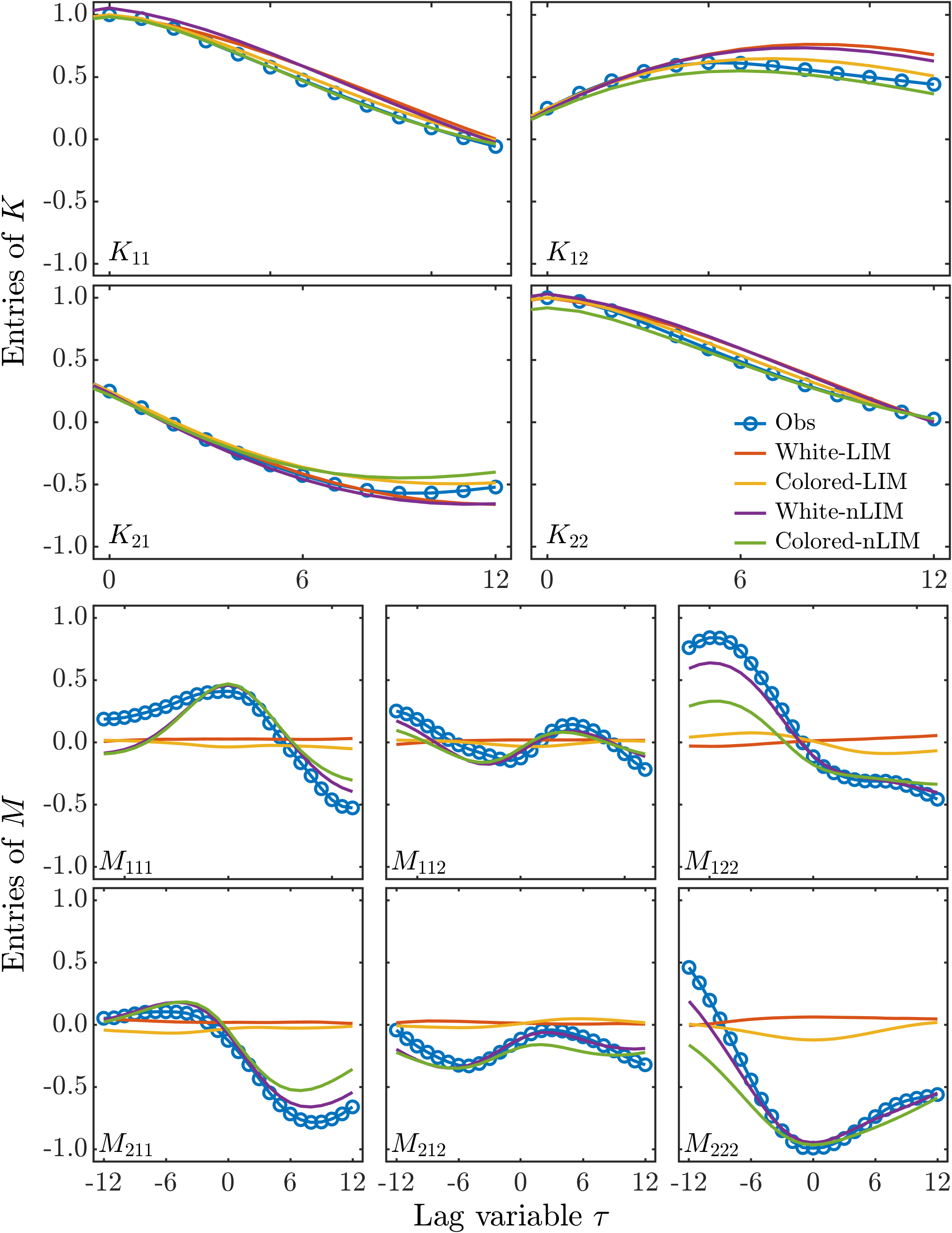
The Linear Inverse Model (LIM) is a class of data-driven methods that construct approximate linear stochastic models to represent complex observational data. The stochastic forcing can be modeled using either Gaussian white noise or Ornstein-Uhlenbeck colored noise; the corresponding models are called White-LIM and Colored-LIM, respectively. Although LIMs are widely applied in climate sciences, they inherently approximate observed distributions as Gaussian, limiting their ability to capture asymmetries. In this study, we extend LIMs to incorporate nonlinear dynamics, introducing White-nLIM and Colored-nLIM which allow for a more flexible and accurate representation of complex dynamics from observations. The proposed methods not only account for the nonlinear nature of the underlying system but also effectively capture the skewness of the observed distribution. Moreover, we apply these methods to a lower-dimensional representation of ENSO and demonstrate that both White-nLIM and Colored-nLIM successfully capture its nonlinear characteristic.