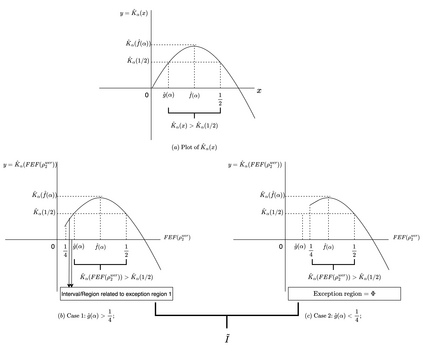
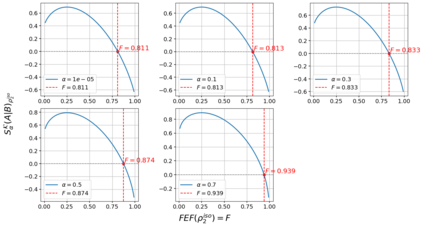
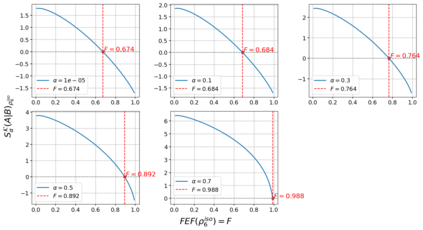
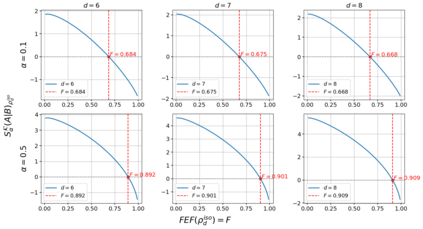
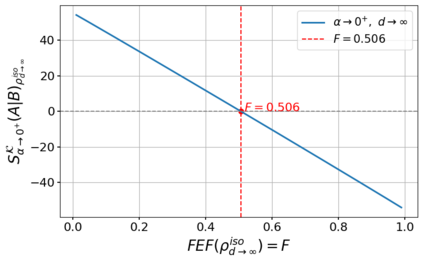
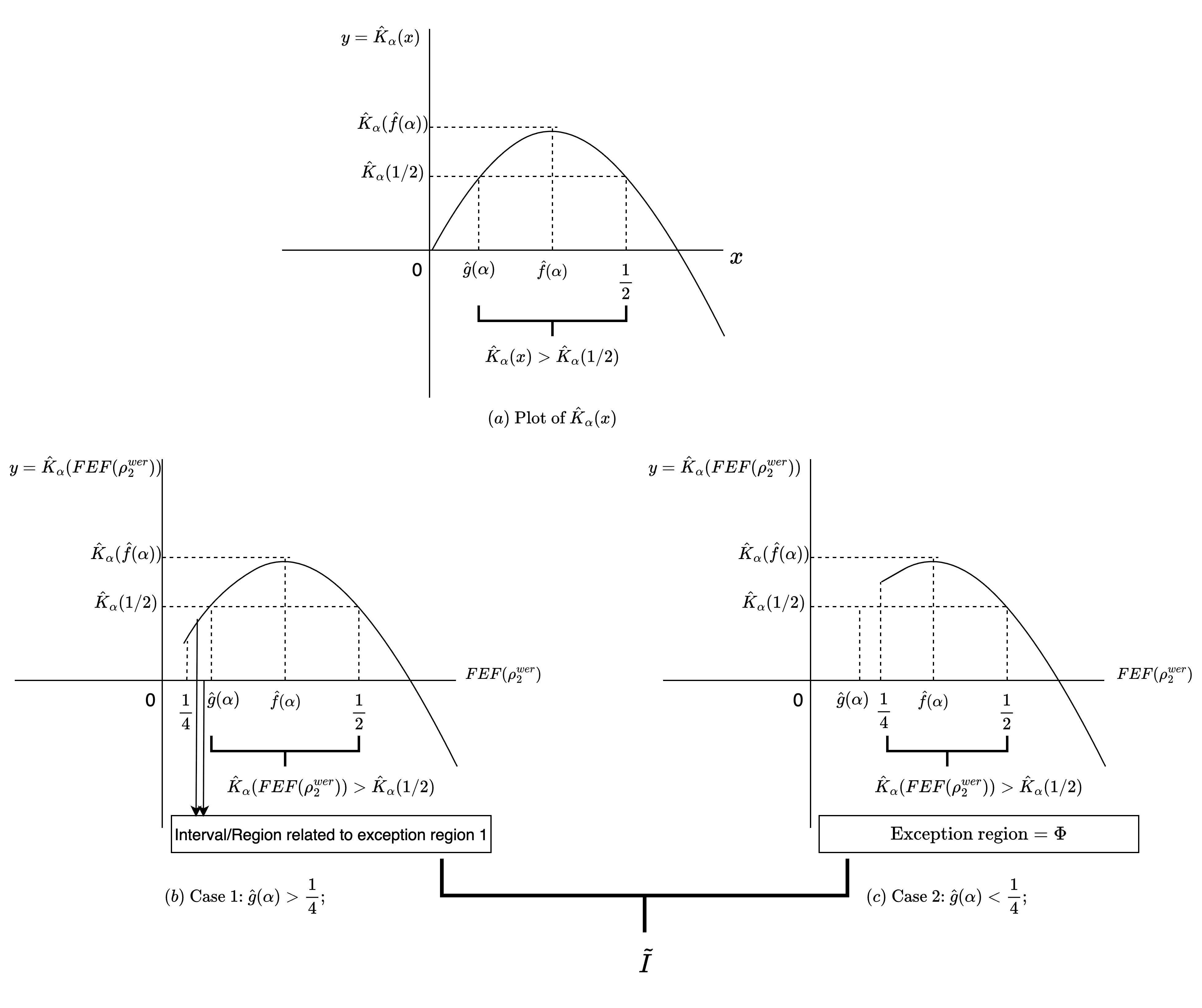
In the present article, we examine the relationship of negative conditional quantum Kaniadakis entropy ($\alpha-$CQKE) with the fully entangled fraction (FEF) which is a substantial yardstick for quantum information processing protocols including teleportation, and quantum steerability, executed over four vital quantum states with maximally mixed marginals, the 2-qubit Werner state, the 2-qubit Weyl state, the 2-qudit Werner state and the isotropic state. We initiate our analysis in 2$\otimes$2 systems where we derive implicit bounds on FEF when the $\alpha-$CQKE takes negative values, i.e. when $\alpha-$CQKE $\in$ $R^{-}$ for 2-qubit Werner state. Consequently, we derive the sufficient implicit bounds for a definitive claim on the non-usefulness of Werner state for quantum teleportation provided its visibility parameter succeeds to elude a critical region, the exception region 1, where the situation becomes inconclusive. Subsequently, we replicate the same for the 2-qubit Weyl state with some constraints augmented by an analogous exception region 2 and the correlation tensor matrix elements. Furthermore, we extend our investigation to d $\otimes$ d states, commencing our analysis with the Isotropic state. We derive implicit bounds on FEF of the Isotropic state and the 2-qudit Werner state resembling the ones in the 2$\otimes$2 analysis. Additionally, we utilize the convoluted relationship between the FEF and quantum steerability to formulate propositions linking negative $\alpha-$CQKE to the k-copy steerability of isotropic states for projective measurements, thereby reducing the intricacy of the study of k-copy steerability directly via FEF. In the appendix section of the article, we provide corroborative calculations and supplementary materials to the theorems presented in the main sections.
翻译:暂无翻译