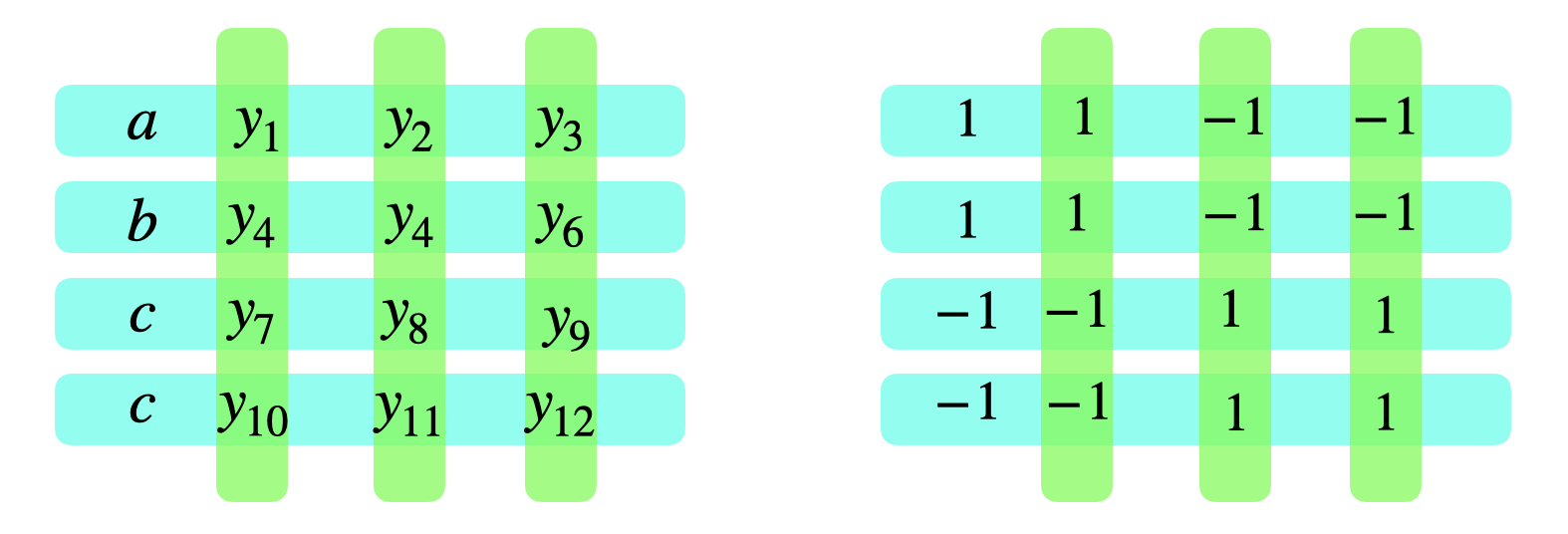
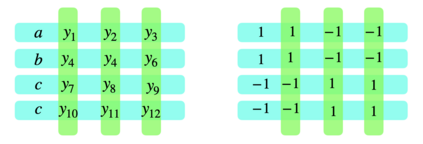
Marcus, Spielman and Srivastava (Annals of Mathematics 2014) solved the Kadison--Singer Problem by proving a strong form of Weaver's conjecture: they showed that for all $\alpha > 0$ and all lists of vectors of norm at most $\sqrt{\alpha}$ whose outer products sum to the identity, there exists a signed sum of those outer products with operator norm at most $\sqrt{8 \alpha} + 2 \alpha.$ We prove that it is NP-hard to distinguish such a list of vectors for which there is a signed sum that equals the zero matrix from those in which every signed sum has operator norm at least $\kappa \sqrt{\alpha}$, for some absolute constant $\kappa > 0.$ Thus, it is NP-hard to construct a signing that is a constant factor better than that guaranteed to exist. For $\alpha = 1/4$, we prove that it is NP-hard to distinguish whether there is a signed sum that equals the zero matrix from the case in which every signed sum has operator norm at least $1/4$.
翻译:Marcus, Spielman和Srivastava(数学年鉴,2014年)通过证明韦佛的强烈猜想形式,证明了Kadison-Singer 问题:它们显示,对于外产产品与身份相当的所有运算方清单,其外产产品与外产产品之比最大相同,这些外产产品的签名总和与操作者标准之比最高为$sqrt{8\alpha}+2\alpha.$我们证明,很难区分这种有签名数的矢量清单,因为对于这些矢量,有签名数的总和等于零矩阵值,而对于每份签名数的运算者,每份运算者标准中至少有$\kappa\srt_alpha}美元,对于某种绝对恒定的美元 > 0美元,因此,很难用NP-rf=1/4美元,我们证明它很难区分在每份标定的运算方中,是否签定了每份数等于0.4美元。