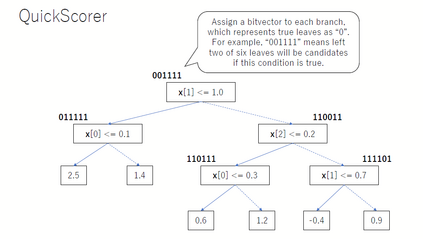
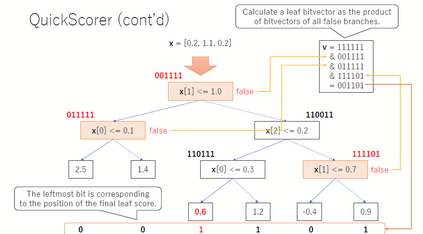
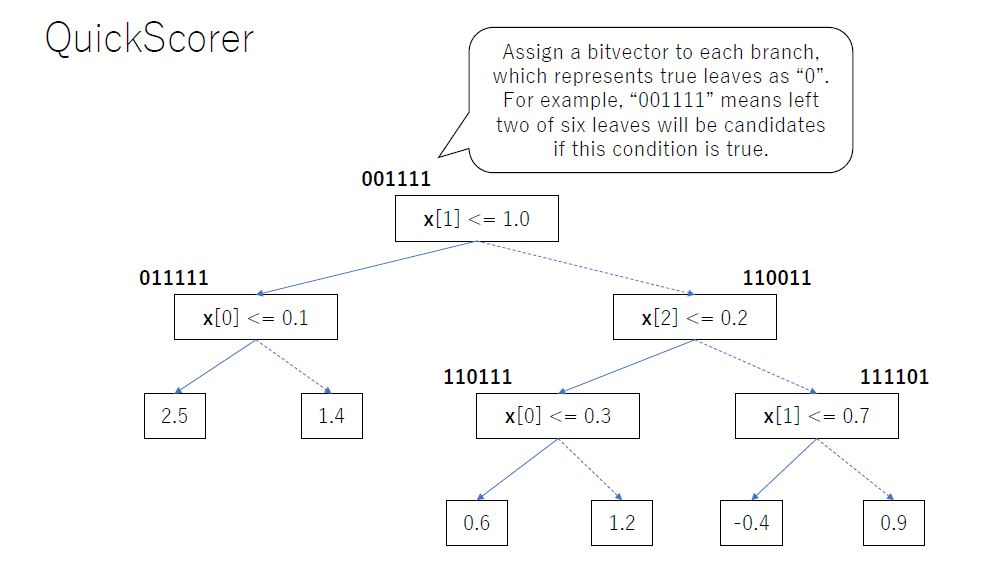
A decision tree looks like a simple computational graph without cycles, where only the leaf nodes specify the output values and the non-terminals specify their tests or split conditions. From the numerical perspective, we express decision trees in the language of computational graph. We explicitly parameterize the test phase, traversal phase and prediction phase of decision trees based on the bitvectors of non-terminal nodes. As shown later, the decision tree is a shallow binary network in some sense. Especially, we introduce the bitvector matrix to implement the tree traversal in numerical approach, where the core is to convert the logical `AND' operation to arithmetic operations. And we apply this numerical representation to extend and unify diverse decision trees in concept.
翻译:决定树看起来像一个简单的计算图,没有周期, 只有叶节点指定输出值和非终点值指定其测试或分割条件。 从数字角度, 我们用计算图的语言表达决定树。 我们根据非终点节点的位子, 明确参数化了决定树的测试阶段、 曲进阶段和预测阶段。 如下文所示, 决定树在某种意义上是一个浅的二进制网络。 特别是, 我们引入了比特维特矩阵, 以数字方式执行树的跨行法, 核心将逻辑的“ AND” 操作转换为算术操作 。 我们用这个数字表示法来扩展和统一概念上不同的决定树 。