Approaches to biological species delimitation based on genetic and spatial dissimilarity

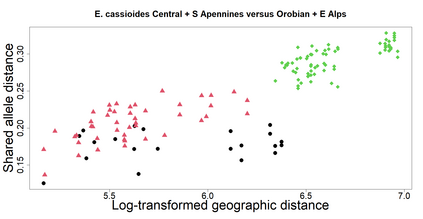
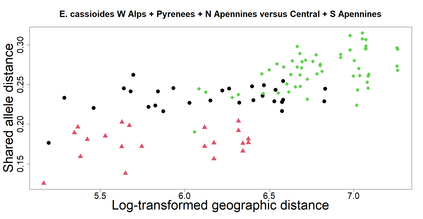
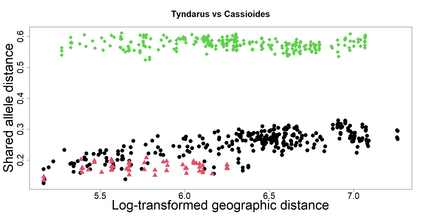
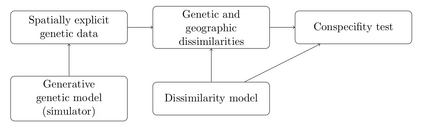
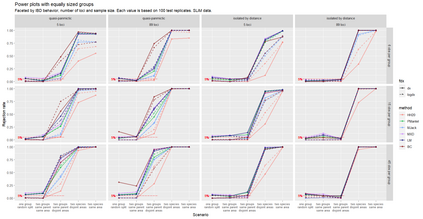
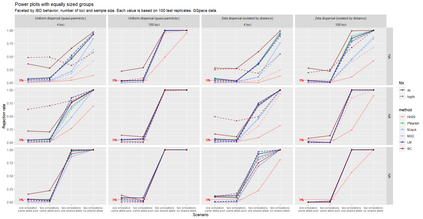
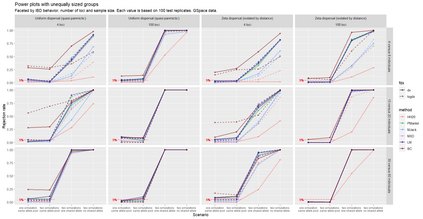
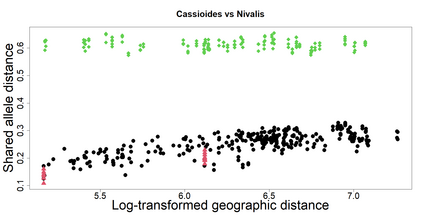
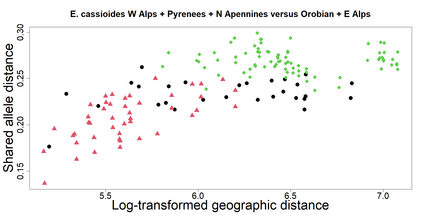
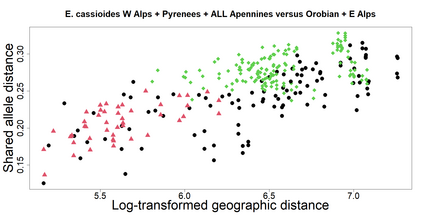
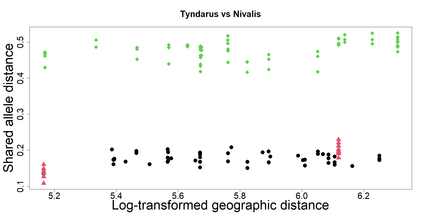
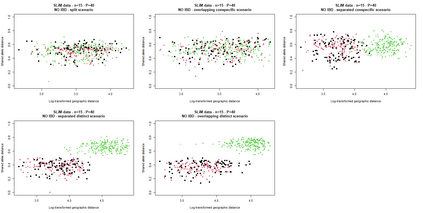
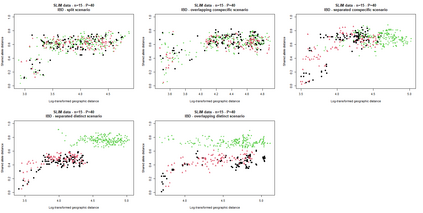
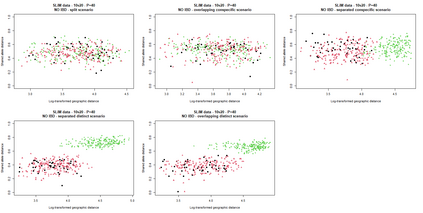
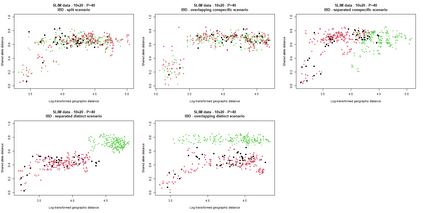
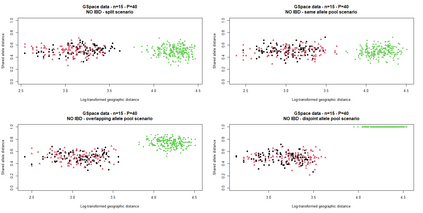
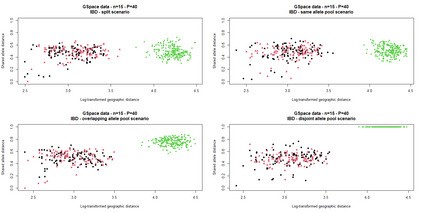
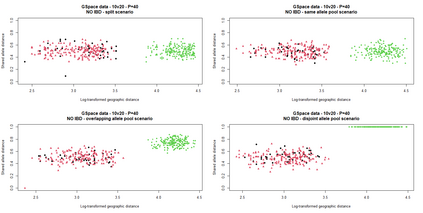
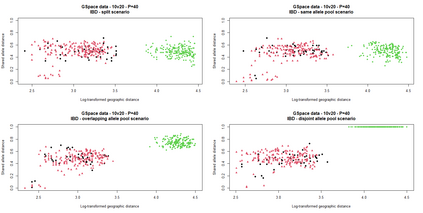
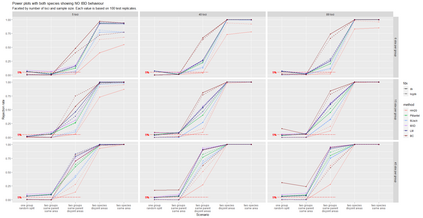
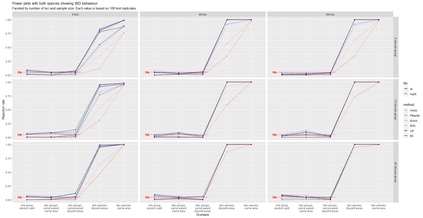
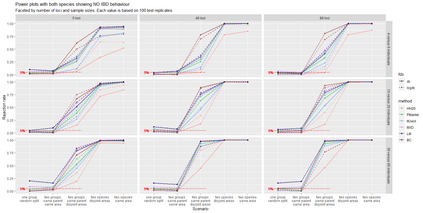
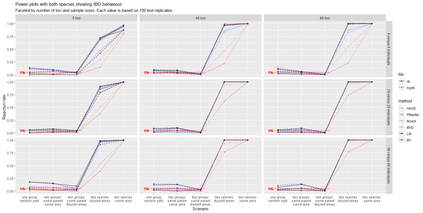
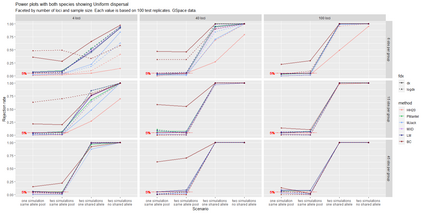
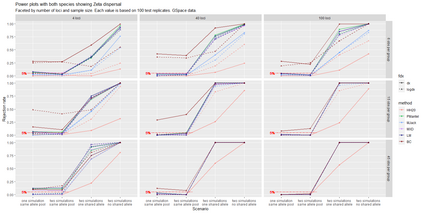
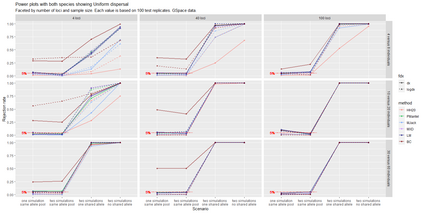
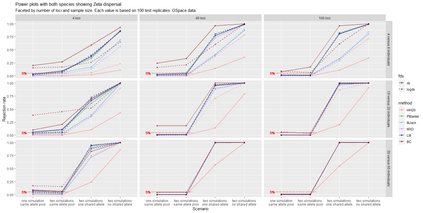
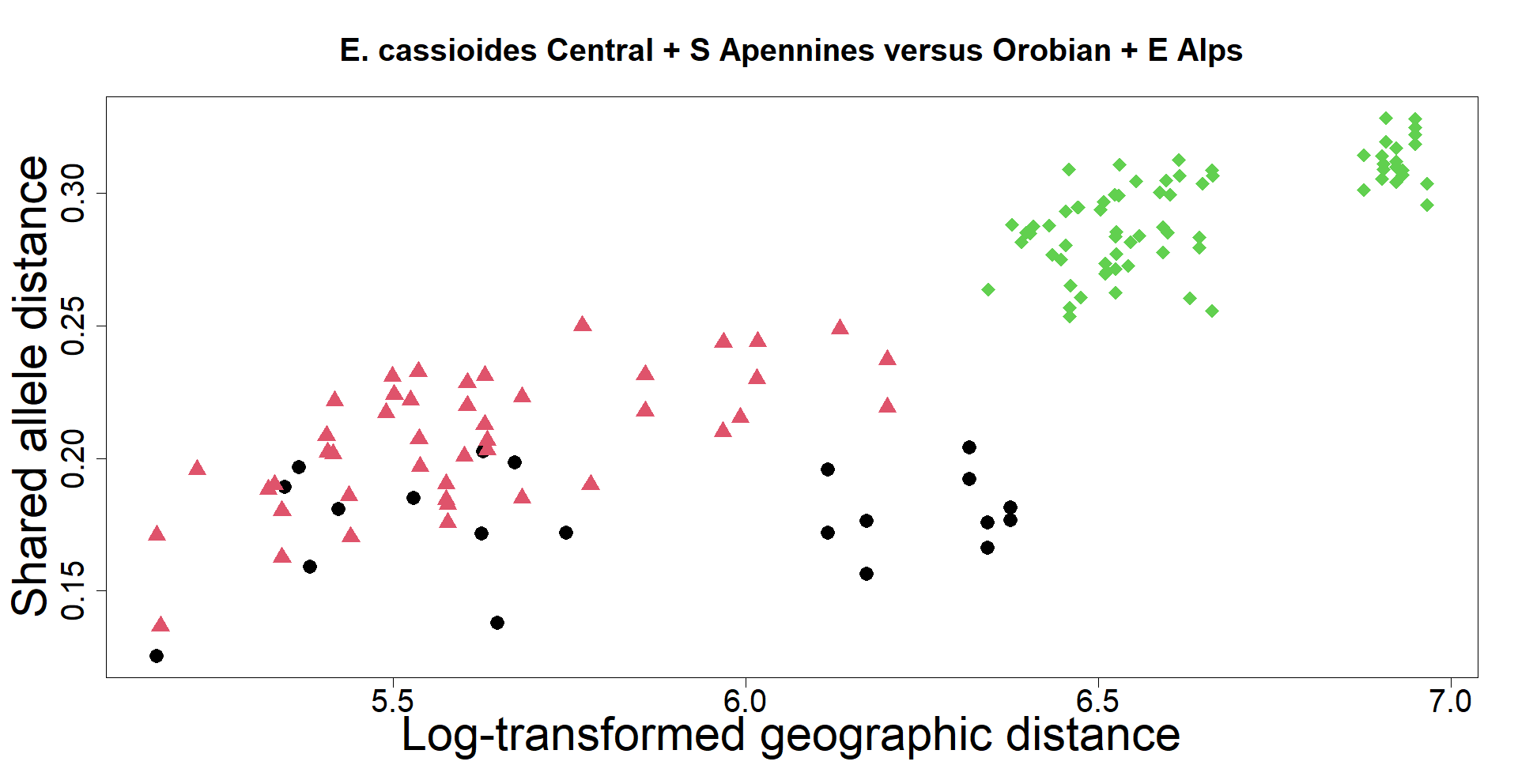
The delimitation of biological species, i.e., deciding which individuals belong to the same species and whether and how many different species are represented in a data set, is key to the conservation of biodiversity. Much existing work uses only genetic data for species delimitation, often employing some kind of cluster analysis. This can be misleading, because geographically distant groups of individuals can be genetically quite different even if they belong to the same species. We investigate the problem of testing whether two potentially separated groups of individuals can belong to a single species or not based on genetic and spatial data. Existing methods such as the partial Mantel test and jackknife-based distance-distance regression are considered as well as new approaches, i.e., an adaptation of a mixed effects model, a bootstrap approach, and a jackknife version of partial Mantel. All these methods address the issue that distance data violate the independence assumption for standard inference regarding correlation and regression; a standard linear regression is also considered. The approaches are compared on simulated meta-populations generated with SLiM and GSpace - two software packages that can simulate spatially-explicit genetic data at an individual level. Simulations showed that partial Mantel tests and mixed-effects models have larger power than jackknife-based methods, but tend to display type I error rates slightly above the significance level. An application on brassy ringlets concludes the paper.