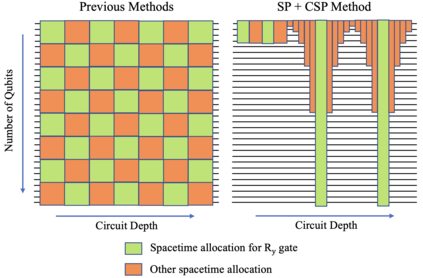
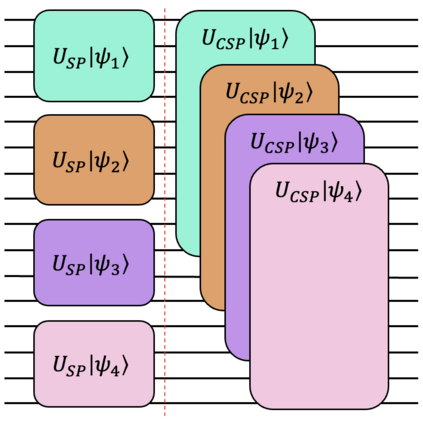
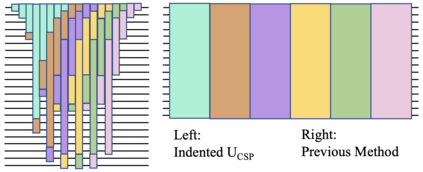
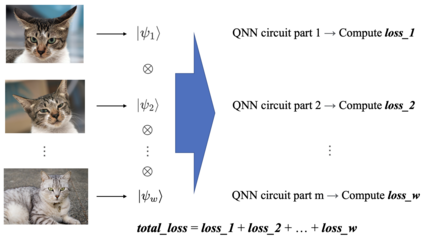
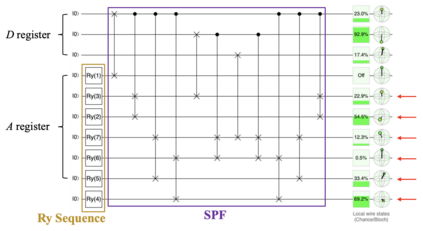
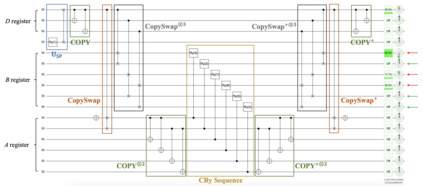
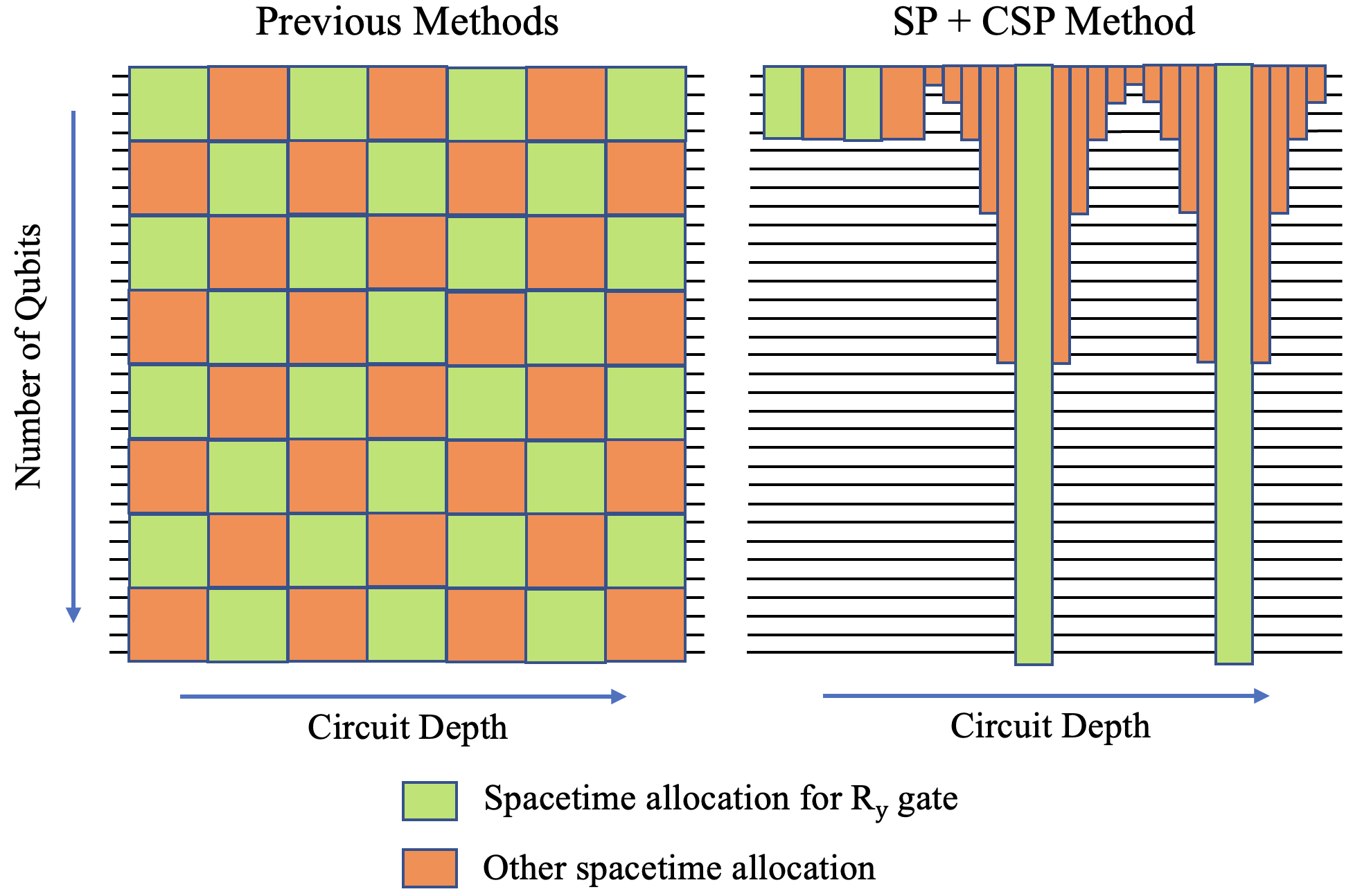
We propose a novel deterministic method for preparing arbitrary quantum states. When our protocol is compiled into CNOT and arbitrary single-qubit gates, it prepares an $N$-dimensional state in depth $O(\log(N))$ and spacetime allocation (a metric that accounts for the fact that oftentimes some ancilla qubits need not be active for the entire circuit) $O(N)$, which are both optimal. When compiled into the $\{\mathrm{H,S,T,CNOT}\}$ gate set, we show that it requires asymptotically fewer quantum resources than previous methods. Specifically, it prepares an arbitrary state up to error $\epsilon$ with optimal depth of $O(\log(N) + \log (1/\epsilon))$ and spacetime allocation $O(N\log(\log(N)/\epsilon))$, improving over $O(\log(N)\log(\log (N)/\epsilon))$ and $O(N\log(N/\epsilon))$, respectively. We illustrate how the reduced spacetime allocation of our protocol enables rapid preparation of many disjoint states with only constant-factor ancilla overhead -- $O(N)$ ancilla qubits are reused efficiently to prepare a product state of $w$ $N$-dimensional states in depth $O(w + \log(N))$ rather than $O(w\log(N))$, achieving effectively constant depth per state. We highlight several applications where this ability would be useful, including quantum machine learning, Hamiltonian simulation, and solving linear systems of equations. We provide quantum circuit descriptions of our protocol, detailed pseudocode, and gate-level implementation examples using Braket.
翻译:暂无翻译