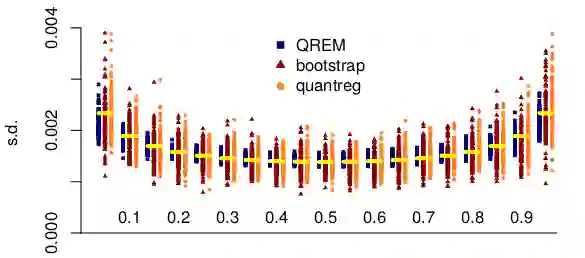
We show that the estimating equations for quantile regression can be solved using a simple EM algorithm in which the M-step is computed via weighted least squares, with weights computed at the E-step as the expectation of independent generalized inverse-Gaussian variables. We compute the variance-covariance matrix for the quantile regression coefficients using a kernel density estimator that results in more stable standard errors than those produced by existing software. A natural modification of the EM algorithm that involves fitting a linear mixed model at the M-step extends the methodology to mixed effects quantile regression models. In this case, the fitting method can be justified as a generalized alternating minimization algorithm. Obtaining quantile regression estimates via the weighted least squares method enables model diagnostic techniques similar to the ones used in the linear regression setting. The computational approach is compared with existing software using simulated data, and the methodology is illustrated with several case studies.
翻译:我们显示,量化回归的估算方程可以通过简单的EM算法来解决,在这种算法中,M级通过加权最小方程计算,在E级计算加权数,作为独立通用反向-Gausian变量的预期值。我们用一个内核密度估测器计算四分位回归系数的差异差差差矩阵,产生比现有软件产生的更稳定的标准错误。对EM级算法进行自然修改,在M级安装一个线性混合模型,将该方法扩大到混合效应四分位回归模型。在这种情况下,适当方法可以作为普遍交替最小化算法进行。通过加权最小方位法获得四分位回归估计,使模型诊断技术与在线性回归设置中使用的方法相类似。计算方法与使用模拟数据的现有软件进行比较,并用若干案例研究来说明该方法。