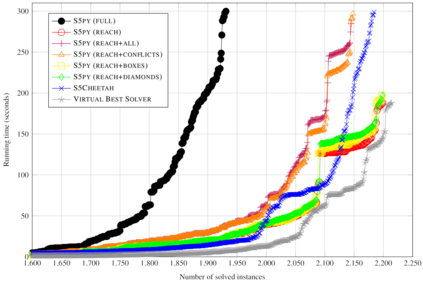
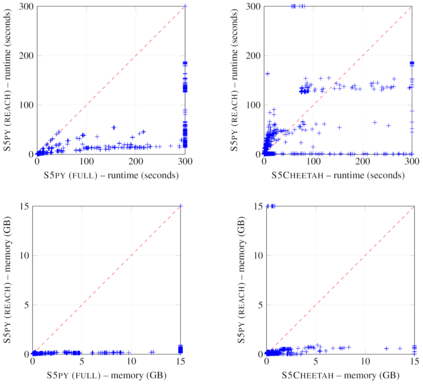
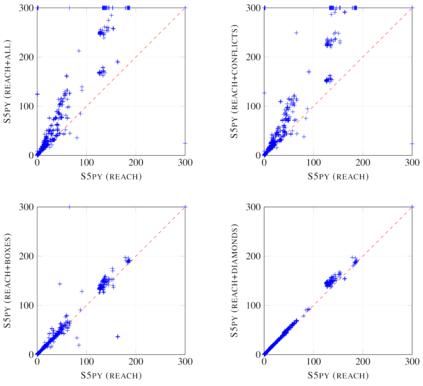
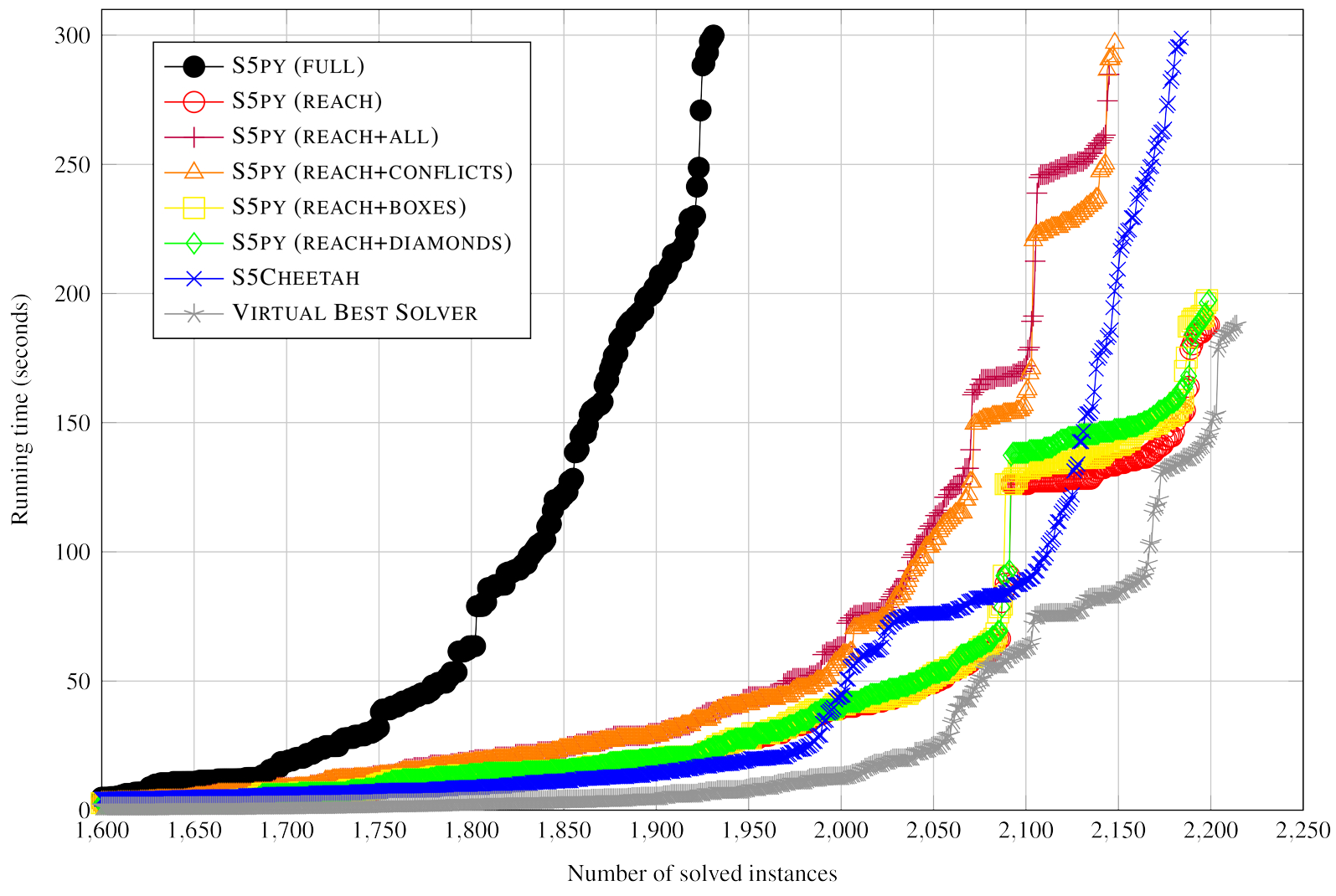
Modal logic S5 has attracted significant attention and has led to several practical applications, owing to its simplified approach to dealing with nesting modal operators. Efficient implementations for evaluating satisfiability of S5 formulas commonly rely on Skolemisation to convert them into propositional logic formulas, essentially by introducing copies of propositional atoms for each set of interpretations (possible worlds). This approach is simple, but often results into large formulas that are too difficult to process, and therefore more parsimonious constructions are required. In this work, we propose to use Answer Set Programming for implementing such constructions, and in particular for identifying the propositional atoms that are relevant in every world by means of a reachability relation. The proposed encodings are designed to take advantage of other properties such as entailment relations of subformulas rooted by modal operators. An empirical assessment of the proposed encodings shows that the reachability relation is very effective and leads to comparable performance to a state-of-the-art S5 solver based on SAT, while entailment relations are possibly too expensive to reason about and may result in overhead. This paper is under consideration for acceptance in TPLP.
翻译:模块逻辑S5吸引了人们的极大关注,并导致了若干实际应用,原因是它简化了处理巢式模型操作者的方法。评估S5公式的可讽刺性的有效实施通常依靠Skolemization将之转化为假设逻辑公式,主要是为每一组解释(可能的世界)引入建议原子的副本。这一方法很简单,但往往导致难以处理的大公式,因此需要更难于处理的构造。在这项工作中,我们提议使用“答案套”程序来实施这些构造,特别是要通过可实现性关系来确定在每一个世界中都具有相关性的参数原子。提议的编码旨在利用其他特性,例如模式操作者所根植的子形体关系。对提议的编码进行经验评估表明,可实现性关系非常有效,并导致与基于SAT的状态的S5解决方案的类似性性能,同时造成关系可能太昂贵,无法通过可实现性能关系来确定,并可能导致间接费用。本文正在考虑在TPL中接受。