Algebra of Nonlocal Boxes and the Collapse of Communication Complexity

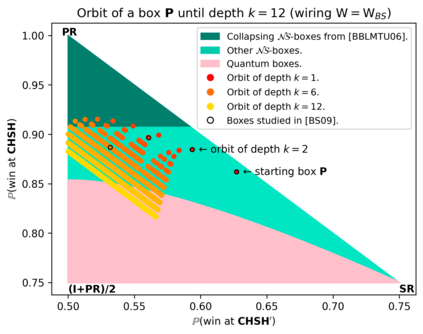
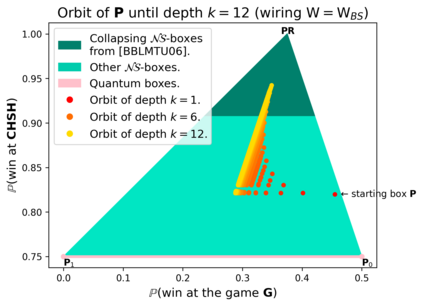
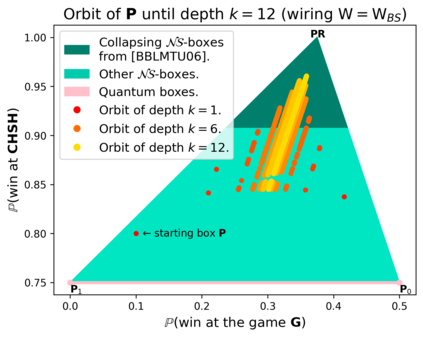
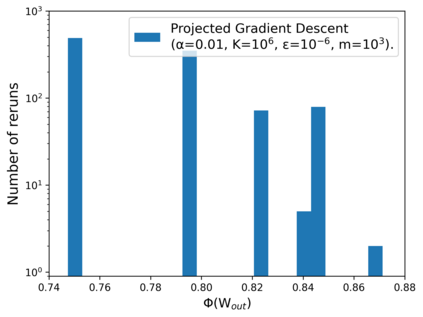
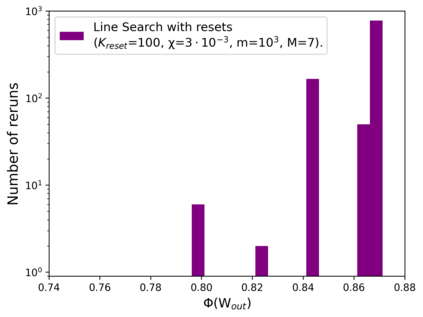
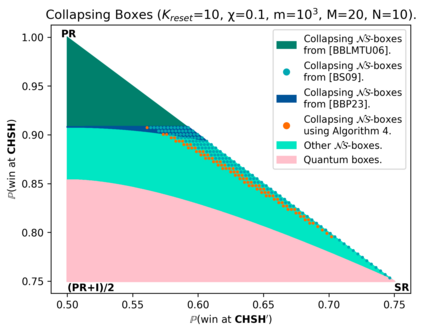
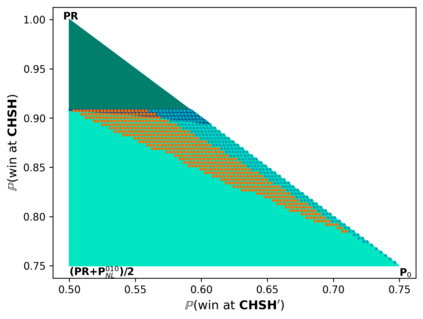
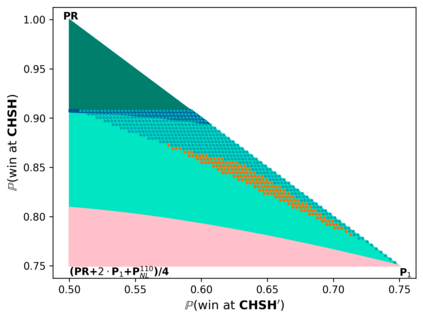
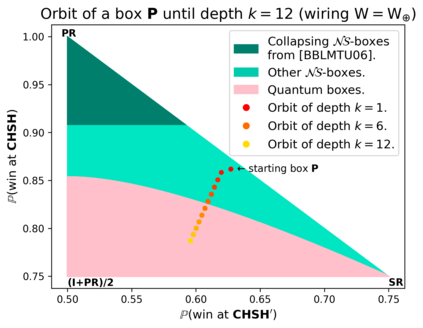
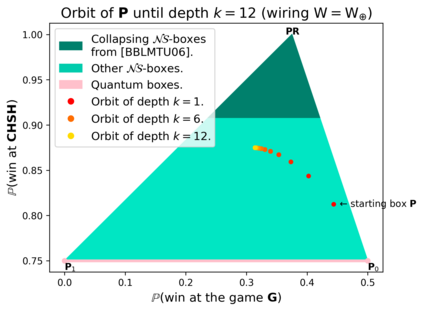
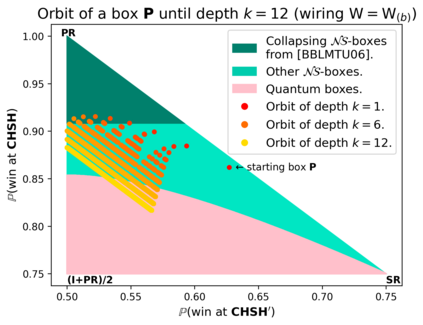
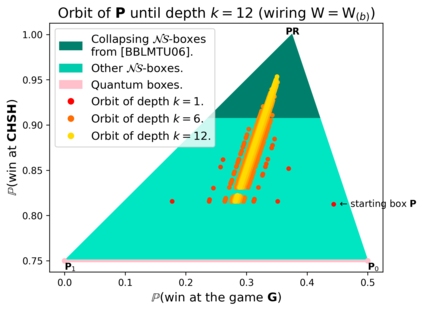
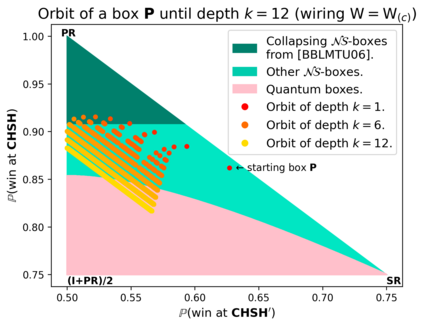
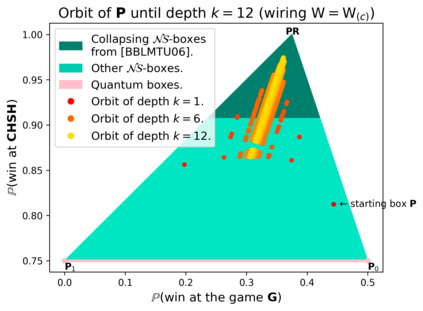
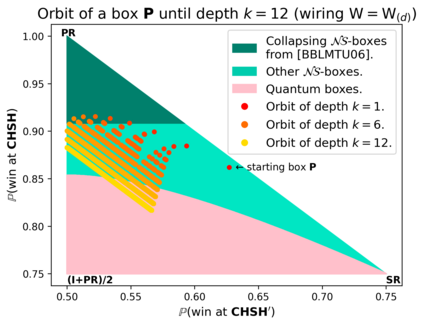
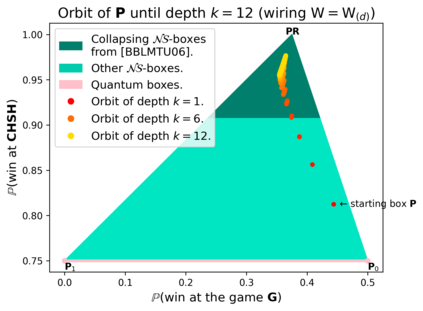
Communication complexity quantifies how difficult it is for two distant computers to evaluate a function $f(X,Y)$ where the strings $X$ and $Y$ are distributed to the first and second computer, respectively and under the constraint of exchanging as few bits as possible. Surprisingly, some nonlocal boxes, which are resources shared by the two computers, are so powerful that they allow to collapse communication complexity, in the sense that any Boolean function $f$ can be correctly estimated with the exchange of only one bit of communication. The Popescu-Rohrlich (PR) box is an example of such a collapsing resource, but a comprehensive description of the set of collapsing nonlocal boxes remains elusive. In this work, we carry out an algebraic study of the structure of wirings connecting nonlocal boxes, thus defining the notion of the "product of boxes" $\mathtt{P}\boxtimes\mathtt{Q}$, and we show related associativity and commutativity results. This gives rise to the notion of the "orbit of a box", unveiling surprising geometrical properties about the alignment and parallelism of distilled boxes. The power of this new framework is that it allows to prove previously-reported numerical intuitions concerning the best way to wire consecutive boxes, and to numerically and analytically recover recently-identified noisy PR boxes that collapse communication complexity for different types of noise models.