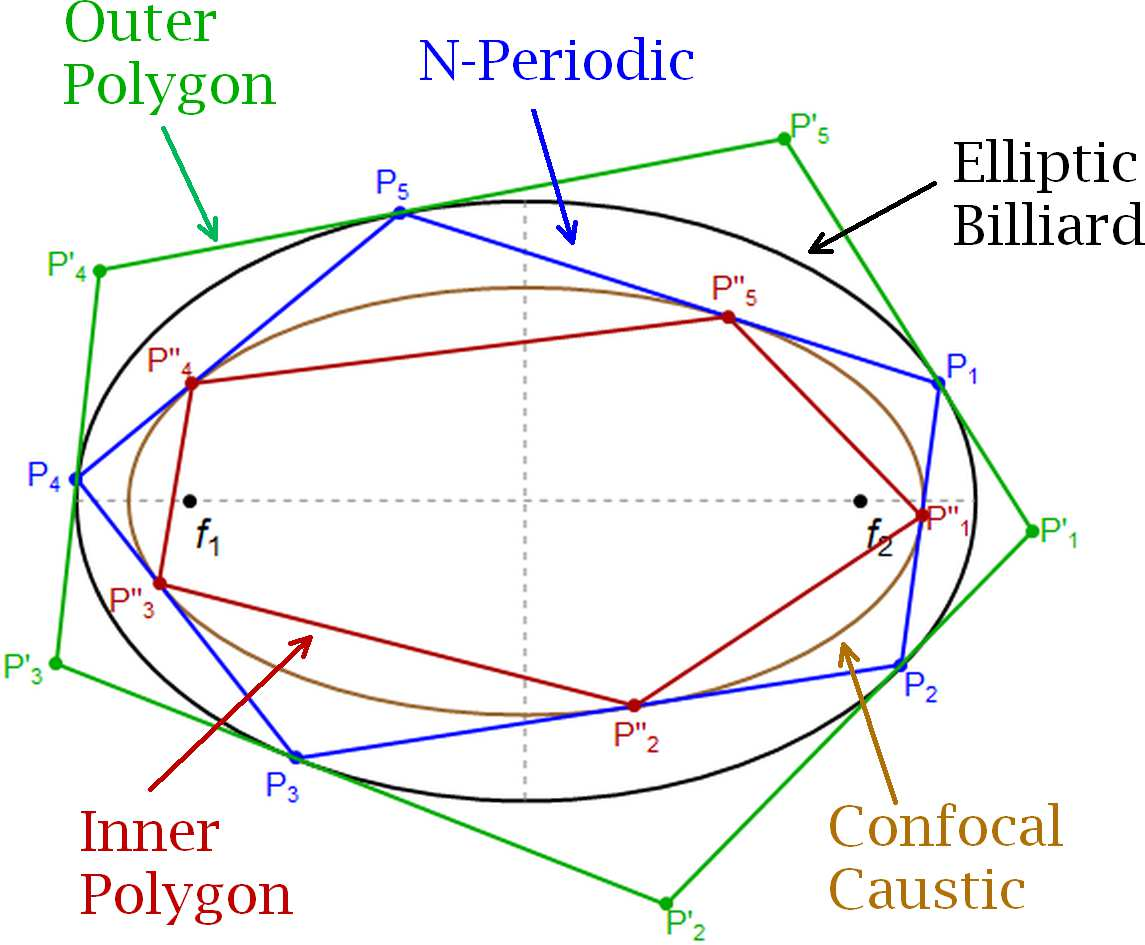
We study self-intersected N-periodics in the elliptic billiard, describing new facts about their geometry (e.g., self-intersected 4-periodics have vertices concyclic with the foci). We also check if some invariants listed in "Eighty New Invariants of N-Periodics in the Elliptic Billiard" (2020), arXiv:2004.12497, remain invariant in the self-intersected case. Toward that end, we derive explicit expressions for many low-N simple and self-intersected cases. We identify two special cases (one simple, one self-intersected) where a quantity prescribed to be invariant is actually variable.
翻译:我们研究在椭圆面板上的自相交叉的N周期,描述有关其几何学的新事实(例如,自相交叉的4周期有与foci相融合的脊椎)。我们还检查“Elliptic Billiard(2020年)中N-Periodics的8-新变异物”(arxiv:2004.12497)中列出的一些变异物是否在自相交叉的案例中始终没有变化。为此,我们为许多低N简单、自相交叉的病例得出了明确的表达方式。我们找出了两种特殊案例(一个简单、一个自我交叉的),在这些特殊案例中,规定在自相交叉的病例中,一定数量是变化不定的。