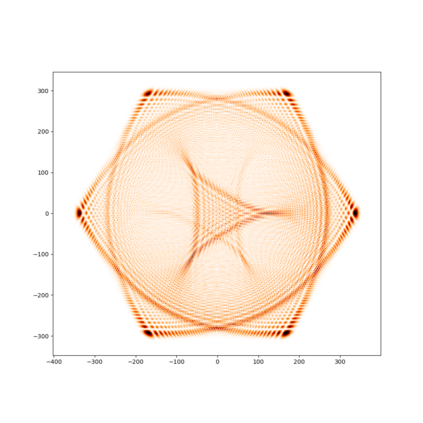
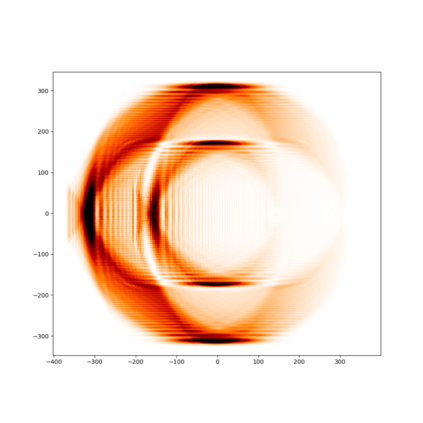
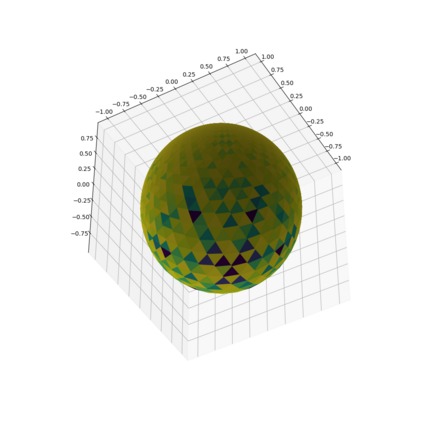
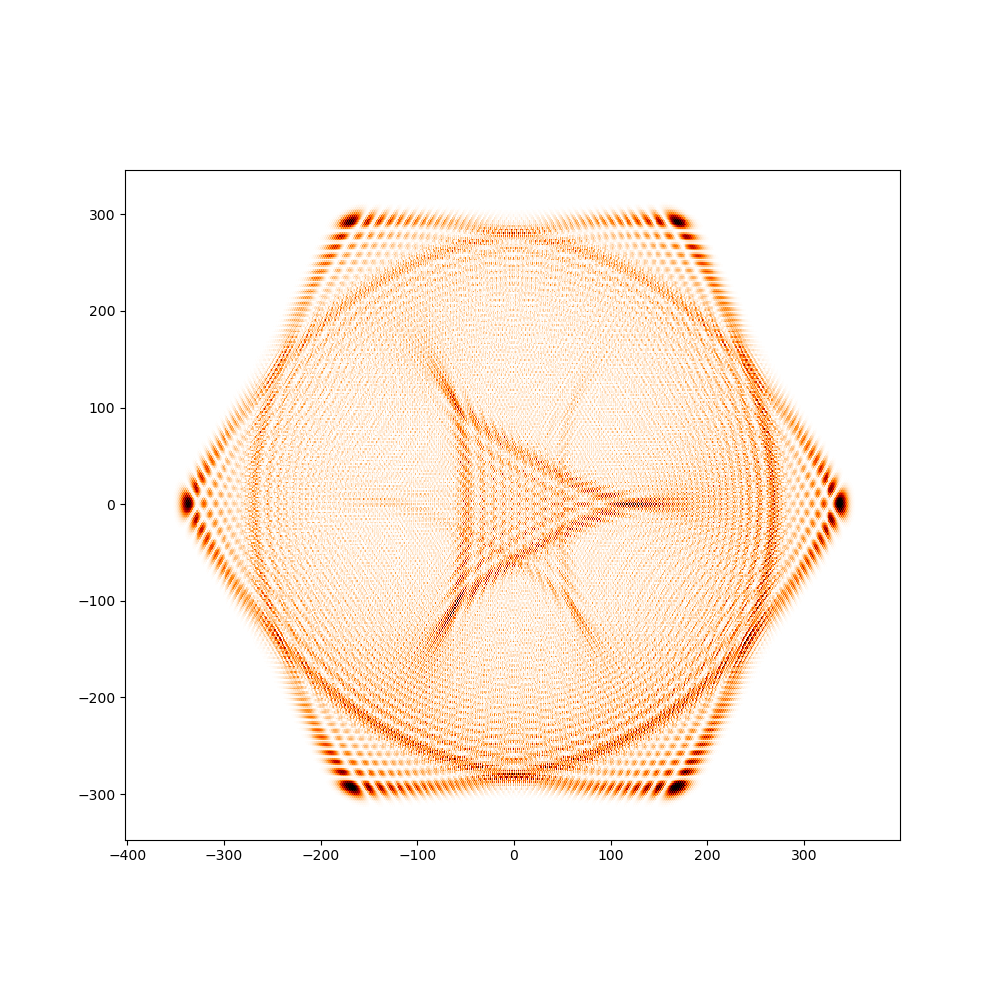
We propose a new family of discrete-spacetime quantum walks capable to propagate on any arbitrary triangulations. Moreover we also extend and generalize the duality principle introduced by one of the authors, linking continuous local deformations of a given triangulation and the inhomogeneity of the local unitaries that guide the quantum walker. We proved that in the formal continuous limit, in both space and time, this new family of quantum walks converges to the (1+2)D massless Dirac equation on curved manifolds. We believe that this result has relevance in both modelling/simulating quantum transport on discrete curved structures, such as fullerene molecules or dynamical causal triangulation, and in addressing fast and efficient optimization problems in the context of the curved space optimization methods.
翻译:我们建议建立一个能够传播任意三角形的离散空间时量子行走新体系。 此外,我们还扩展并推广其中一位作者提出的双重性原则,将特定三角形的连续局部变形与引导量子行走器的地方单位的不相容性联系起来。我们证明,在正式的连续限制中,无论是在时间还是时间上,这种新的量子行走组合都与曲线形体上的(1+2)D无质量Dirac方程相融合。 我们认为,这一结果与在离散曲线形结构上建模/模拟量子传输有关,如更远分子或动态因果三角,以及在曲线形空间优化方法中快速和高效地优化问题。
相关内容
Source: Apple - iOS 8