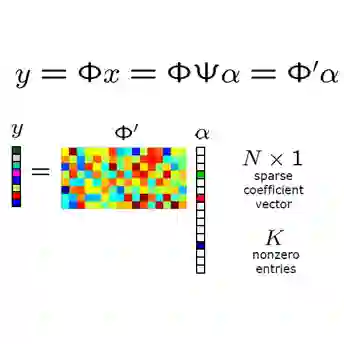
Compressive sensing involves the inversion of a mapping $SD \in \mathbb{R}^{m \times n}$, where $m < n$, $S$ is a sensing matrix, and $D$ is a sparisfying dictionary. The restricted isometry property is a powerful sufficient condition for the inversion that guarantees the recovery of high-dimensional sparse vectors from their low-dimensional embedding into a Euclidean space via convex optimization. However, determining whether $SD$ has the restricted isometry property for a given sparisfying dictionary is an NP-hard problem, hampering the application of compressive sensing. This paper provides a novel approach to resolving this problem. We demonstrate that it is possible to derive a sensing matrix for any sparsifying dictionary with a high probability of retaining the restricted isometry property. In numerical experiments with sensing matrices for K-SVD, Parseval K-SVD, and wavelets, our recovery performance was comparable to that of benchmarks obtained using Gaussian and Bernoulli random sensing matrices for sparse vectors.
翻译:压缩感应涉及调制 $SD $SD $@in mathbb{R ⁇ m\ times n} 美元的反向, 美元 < n$, 美元是一个感应矩阵, 美元是一本神秘字典。 限制的等量属性是使高维稀散矢量通过convex优化从低维嵌入 Euclidean 空间中恢复的强大条件。 然而, 确定 $SD 是否具有给定的显微字典的限值等值属性是一个硬性的问题, 妨碍压缩感应的应用。 本文为解决这一问题提供了一种新颖的方法。 我们证明, 有可能为任何彩色字典绘制一种感应矩阵, 很有可能保留限制的量度属性。 在对 K- SVD、 Parseval K- SVD 和波子的感测矩阵进行的数字实验中, 我们的恢复性能与使用高尔斯和伯努利随机遥感基质矢量矢量测量基取得的基准相当。