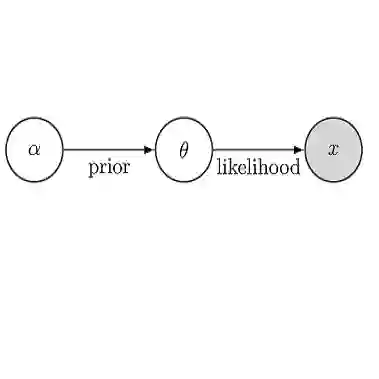
We study the implementation of Automatic Differentiation Variational inference (ADVI) for Bayesian inference on regression models with bridge penalization. The bridge approach uses $\ell_{\alpha}$ norm, with $\alpha \in (0, +\infty)$ to define a penalization on large values of the regression coefficients, which includes the Lasso ($\alpha = 1$) and ridge $(\alpha = 2)$ penalizations as special cases. Full Bayesian inference seamlessly provides joint uncertainty estimates for all model parameters. Although MCMC aproaches are available for bridge regression, it can be slow for large dataset, specially in high dimensions. The ADVI implementation allows the use of small batches of data at each iteration (due to stochastic gradient based algorithms), therefore speeding up computational time in comparison with MCMC. We illustrate the approach on non-parametric regression models with B-splines, although the method works seamlessly for other choices of basis functions. A simulation study shows the main properties of the proposed method.
翻译:暂无翻译