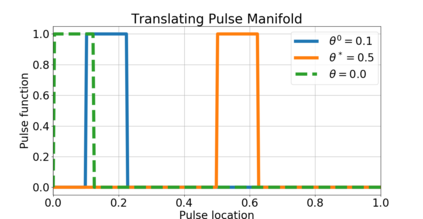
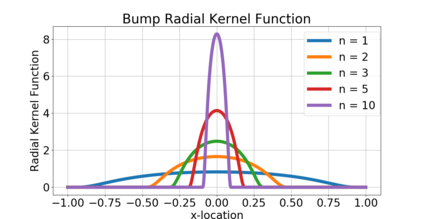
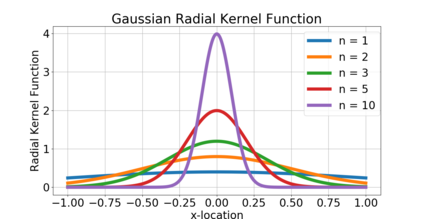
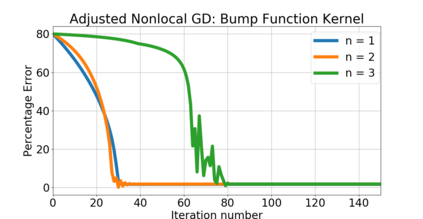
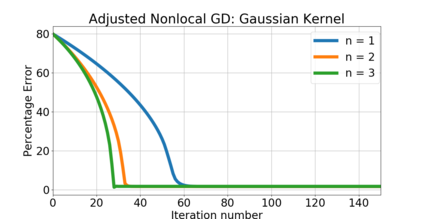
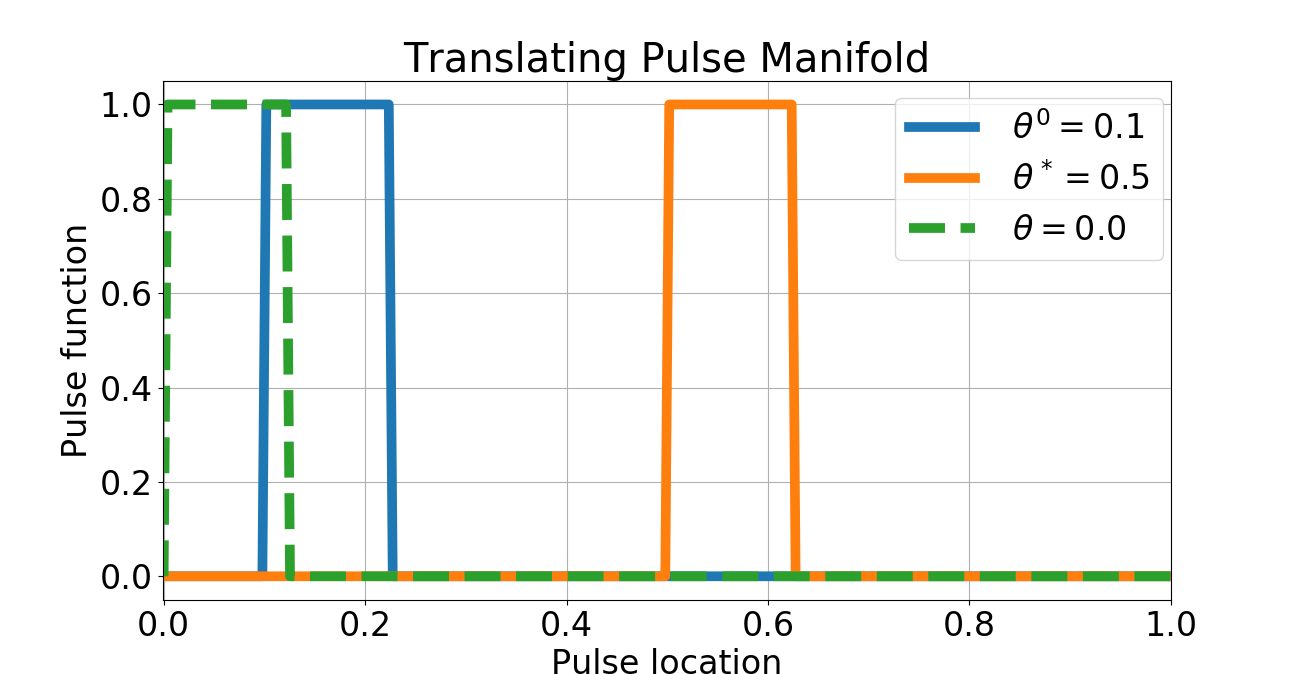
Nonlocal models have recently had a major impact in nonlinear continuum mechanics and are used to describe physical systems/processes which cannot be accurately described by classical, calculus based "local" approaches. In part, this is due to their multiscale nature that enables aggregation of micro-level behavior to obtain a macro-level description of singular/irregular phenomena such as peridynamics, crack propagation, anomalous diffusion and transport phenomena. At the core of these models are nonlocal differential operators, including nonlocal analogs of the gradient/Hessian. This paper initiates the use of such nonlocal operators in the context of optimization and learning. We define and analyze the convergence properties of nonlocal analogs of (stochastic) gradient descent and Newton's method on Euclidean spaces. Our results indicate that as the nonlocal interactions become less noticeable, the optima corresponding to nonlocal optimization converge to the "usual" optima. At the same time, we argue that nonlocal learning is possible in situations where standard calculus fails. As a stylized numerical example of this, we consider the problem of non-differentiable parameter estimation on a non-smooth translation manifold and show that our nonlocal gradient descent recovers the unknown translation parameter from a non-differentiable objective function.
翻译:最近,非本地模型对非线性连续力力学产生了重大影响,并被用于描述物理系统/过程,这些系统/过程无法用传统的基于“本地”的微积分法准确描述,部分是由于这些模型具有多尺度性,能够将微观行为汇总到宏观一级,从而获得对单/非常规现象的描述,如潜伏动力学、裂变传播、异常扩散和运输现象。这些模型的核心是非本地差异操作员,包括梯度/赫西安的非本地类比。本文在优化和学习方面开始使用此类非本地操作员。我们定义和分析非本地(随机)梯度下行和牛顿方法等类似物在尤科里德空间的趋同特性。我们的结果表明,由于非本地互动越来越不明显,与非本地优化相对应的opima 与“usual” opima 相融合。 同时,我们认为,在标准计算失败的情况下,非本地学习是可能的。作为这一(感官化的)数字化的示例,我们从这种(感化)梯度梯度下,我们从不可辨测的多元性参数上展示了不可辨测测测测的多度参数的、不测地的代位性参数问题。