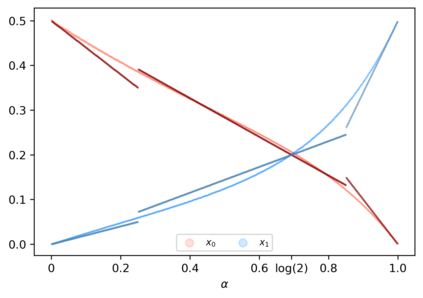
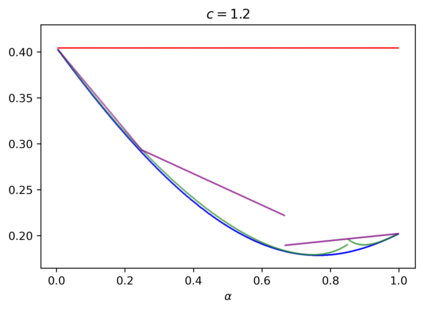
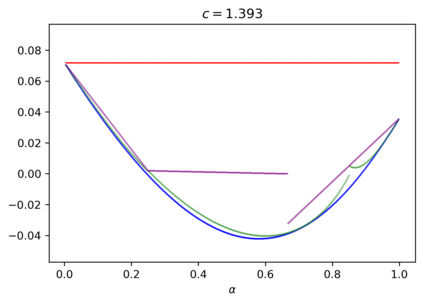
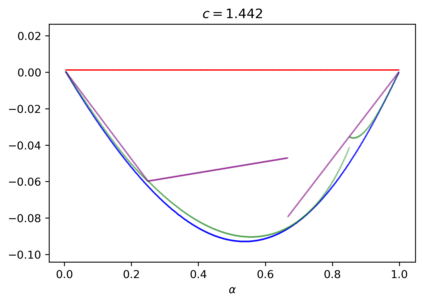
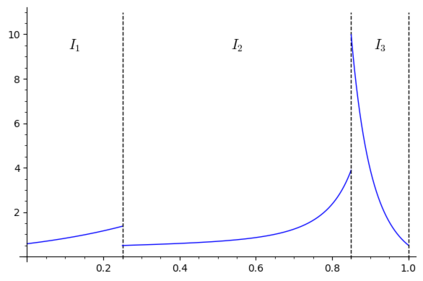
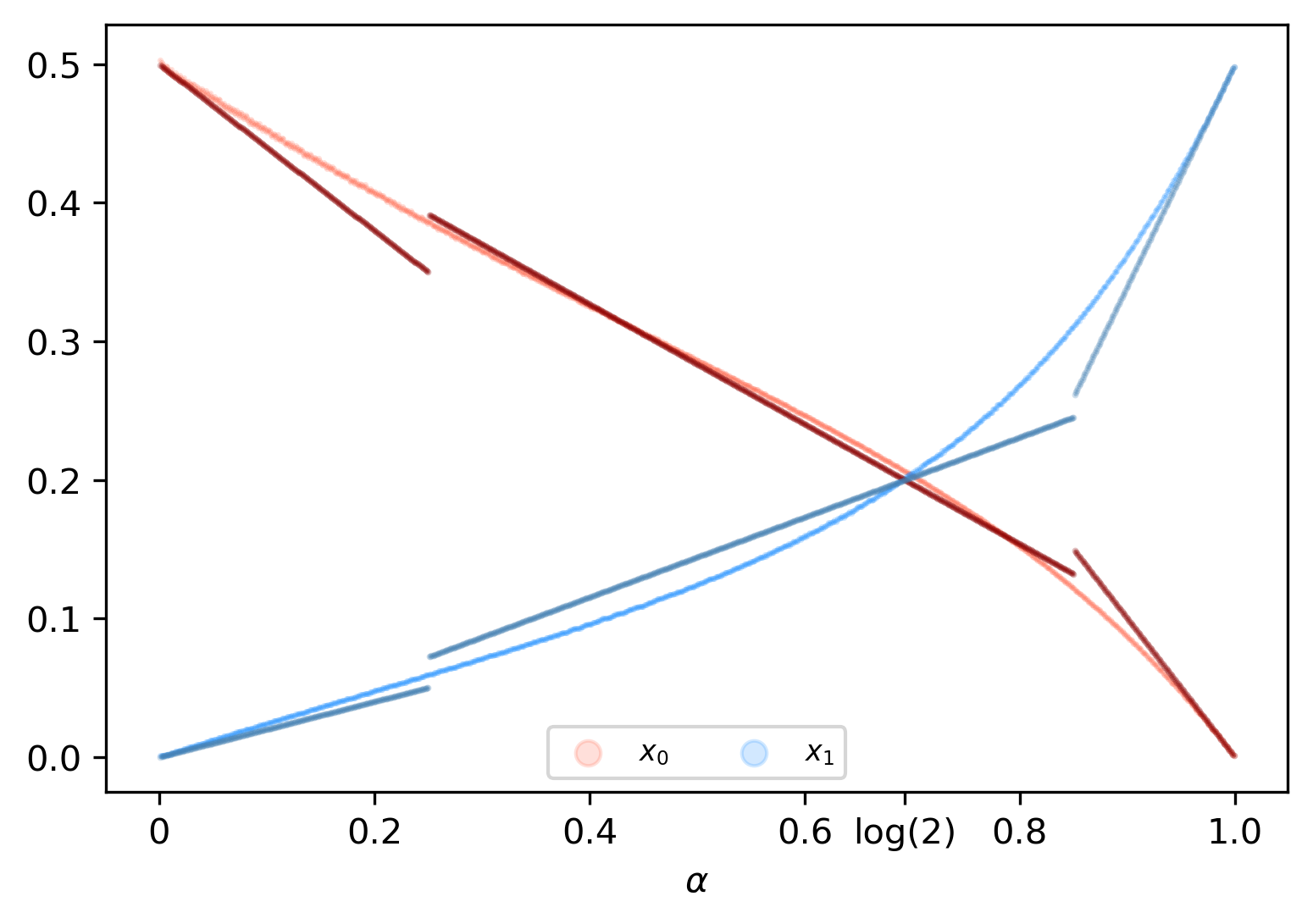
We study the group testing problem where the goal is to identify a set of k infected individuals carrying a rare disease within a population of size n, based on the outcomes of pooled tests which return positive whenever there is at least one infected individual in the tested group. We consider two different simple random procedures for assigning individuals to tests: the constant-column design and Bernoulli design. Our first set of results concerns the fundamental statistical limits. For the constant-column design, we give a new information-theoretic lower bound which implies that the proportion of correctly identifiable infected individuals undergoes a sharp "all-or-nothing" phase transition when the number of tests crosses a particular threshold. For the Bernoulli design, we determine the precise number of tests required to solve the associated detection problem (where the goal is to distinguish between a group testing instance and pure noise), improving both the upper and lower bounds of Truong, Aldridge, and Scarlett (2020). For both group testing models, we also study the power of computationally efficient (polynomial-time) inference procedures. We determine the precise number of tests required for the class of low-degree polynomial algorithms to solve the detection problem. This provides evidence for an inherent computational-statistical gap in both the detection and recovery problems at small sparsity levels. Notably, our evidence is contrary to that of Iliopoulos and Zadik (2021), who predicted the absence of a computational-statistical gap in the Bernoulli design.
翻译:我们研究群体测试问题,我们的目标是根据综合测试的结果,在测试组中至少有一名受感染者时返回正数。我们考虑分配个人进行测试的两个不同的简单随机程序:常数柱设计和Bernoulli设计。我们第一组结果涉及基本统计限度。对于常数柱设计,我们给出一个新的信息理论下限,这意味着正确识别的感染者比例在测试数量跨过特定阈值时会经历“全无”阶段过渡。对于伯努利设计,我们确定解决相关检测问题所需的测试的确切数量(目的是区分群体测试实例和纯噪音),改善特龙、阿尔德里奇和斯卡利特的上限和下限(202020年)。对于两个群体测试模型,我们还研究计算效率(极短时间)的临界差距程序。我们确定低度测试的准确数量,在低度测试设计中,为低度检测水平的直径比值测算提供一个直数,为低度测算的精确度水平。