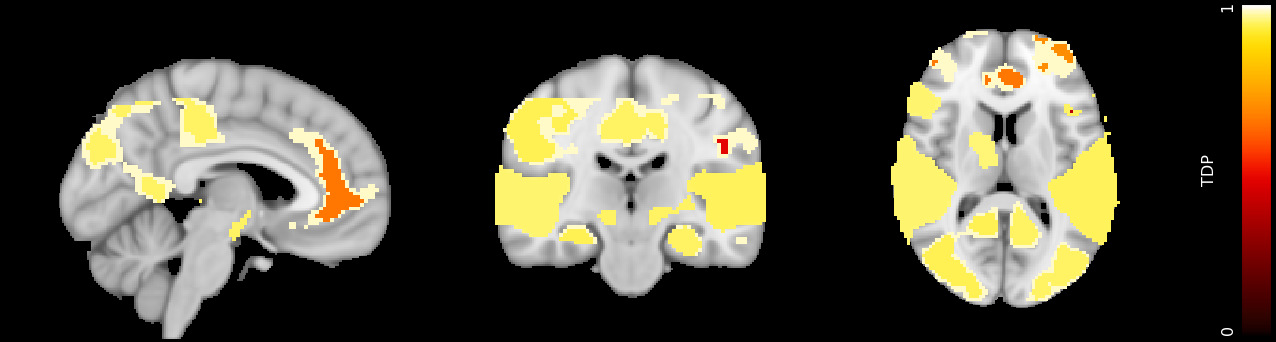
Sum-based global tests are highly popular in multiple hypothesis testing. In this paper we propose a general closed testing procedure for sum tests, which provides lower confidence bounds for the proportion of true discoveries (TDP), simultaneously over all subsets of hypotheses. These simultaneous inferences come for free, i.e., without any adjustment of the alpha-level, whenever a global test is used. Our method allows for an exploratory approach, as simultaneity ensures control of the TDP even when the subset of interest is selected post hoc. It adapts to the unknown joint distribution of the data through permutation testing. Any sum test may be employed, depending on the desired power properties. We present an iterative shortcut for the closed testing procedure, based on the branch and bound algorithm, which converges to the full closed testing results, often after few iterations; even if it is stopped early, it controls the TDP. We compare the properties of different choices for the sum test through simulations, then we illustrate the feasibility of the method for high dimensional data on brain imaging and genomics data.
翻译:在多个假设测试中,基于总和的全球测试非常普遍。 在本文中, 我们提议了一种普通封闭测试程序, 用于总和测试, 它为真实发现的比例提供了较低的信任度, 在所有假设子集中同时提供。 这些同时的推论是免费的, 也就是说, 在使用全球测试时, 无需对阿尔法水平作任何调整。 我们的方法允许一种探索性方法, 因为同时性可以确保TDP的控制权, 即使是当兴趣子集是临时选择时。 它适合通过超常测试对数据进行未知的联合分配。 任何总测试都可以使用, 取决于想要的功率特性。 我们根据分支和约束算法对封闭测试程序提出一个迭接捷径, 它通常在很少的迭代数之后, 与完全封闭测试结果趋同; 即使它被早期停止, 它也控制 TDP 。 我们通过模拟来比较对总和测试的不同选择的特性, 然后我们说明大脑成像和基因组数据高维数据的方法的可行性。